Topología
No número anterior mencionamos a área de Topología e diciamos que era una rama matemática que estuda as propiedades xeométricas inmutables aos rizos e estiramentos.
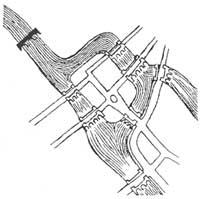
Un problema de Topología: pódese converter a cámara dun pneumático (é dicir, sacar o interior ao exterior e meter o exterior ao interior) sen cortar nin perforar a cámara?
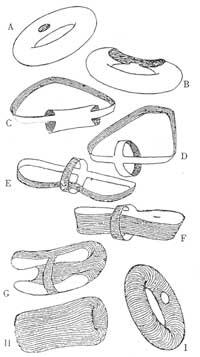
Mentres na práctica teriamos que dicir que non, en Topología diremos que si. Como dixemos na Topología os obxectos pódense rizar e tirar como se queira. Paira darlle a volta á cámara hai que seguir as seguintes instrucións (recomendámosche que non o tentes coa cámara real): indicaremos que o orificio que aparece na imaxe é o lugar no que se coloca a válvula; colocando un dedo no buraco hai que estendelo cada vez máis (A,B) ata que a cámara toma a forma das dúas bandas de goma unidas (C,D); cada tira dá a volta a cada tira é a normal ata que se dá a parte externa. Ten en conta que a dirección das estrías da cámara cambiou. Si ao principio estaban pola cámara, agora pódense ver en dirección perpendicular. Así que demos a volta á cámara. As cámaras iniciais e finais en topología son iguais.
Este tipo de problemas son os que dan á Topología a outra aparencia, xa que parecen enmascarar este novo campo das Matemáticas. No número 29 falámosche da cinta de Möbius e da botella de Klein, os mellores xoguetes dos topólogos.
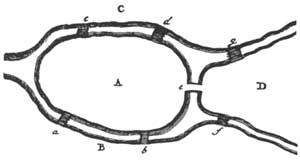
Desde un punto de vista histórico, Leibniz descubriu inicialmente este novo campo das Matemáticas e denominouno expresamente “Analysis Situs”. Máis tarde incorporouse á historia da Topología o nome doutro importante matemático, Leonhard Euler. A anécdota xa é coñecida e XVIII. No século XX sitúase na cidade de Koenigsberg. O río Pregel que pasa por esta cidade era cruzado por sete pontes que unían as beiras do río coas dúas illas (como se pode apreciar na figura 2). Á xente da zona gustáballe, desde hai tempo, tentar pasar una soa vez polas sete pontes. A pesar dos ensaios e ensaios realizados, non atoparon solución ao problema.
Cando o problema chegou a mans de Euler en 1736, pronto se deu conta de que a solución non estaba no cálculo dalgunha medida. E que non se podía resolver mediante cálculos cuantitativos. A posición dos territorios e pontes determina a natureza do problema. Sabía que si se probasen todas as posibilidades de cruzar as sete pontes, una a unha, podíase dar una resposta correcta, pero el non o fixo. Por unha banda era un método aburrido e doutra banda a solución non serviría paira outros problemas.
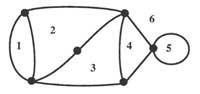
Imos substituír, por exemplo, os territorios por puntos e as liñas que unen as pontes dous puntos. Así obtemos os gráficos da figura 3. Pode pensarse que as distancias entre puntos ou as lonxitudes das vías non inflúen na resolución do problema. A formulación agora sería o seguinte: os “grafos” ou “redes” que ven na figura 3, sen que o bolígrafo deslícese da páxina, deben facerse sen pasar dúas veces por cada vía.
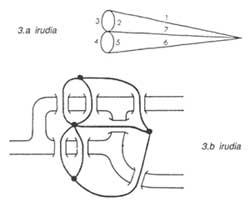
Na solución ideada por Euler, tivo en conta o número de pontes entre diferentes territorios. Podes atopar a solución adaptada no número 13 da revista Elhuyar.
Este problema é sen beizos o exemplo máis famoso da Teoría de Grafos. A Teoría de Grafos ten as súas raíces no estudo de problemas de Topología que poden describirse mediante os puntos denominados vértices e as súas relacións (esquinas). Euler deu relacións entre o número de vértices, arestas e lados, sendo a diferenza a rexión na que a rede ou o grafo divide a superficie. Dita relación é nE + nA = ne + 2, nE = número de vértices, nA = número de lados e ne = número de bordos. Esta fórmula serve paira describir a relación entre o número de vértices, arestas e lados dun poliedro.
Na actualidade a Teoría de Grafos é independente da Topología e ten numerosas aplicacións fóra das Matemáticas: Física teórica, Técnica, Teoría da Rede, etc.
Pola senda dos grafos podemos achegarnos a outro tema fascinante da Topología, o “Problema das catro cores”.
Cando se imprimen mapas políticos, as estatuas contiguas píntanse con distintas cores. Na Topología ou na Teoría de Grafos enténdese por mapa a imaxe formada por cantos, vértices e porcións xeradas na esfera ou plano por un grafo de número finito de cantos. A zona conectada e os bordos que a delimitan (límites) denomínanse Pobos. (Na figura 5 represéntanse catro pobos). Diremos que dous municipios son lindeiros si teñen un bordo común. Debes tomar os conceptos anteriores para que comprendamos ben a cuestión. O “problema das catro cores” non era máis que una conxectura e dicía que todo mapa formado por conexións populares, a pesar da súa complexidade, pódese pintar en catro cores, nos que dous pobos veciños sempre toman dúas cores diferentes.
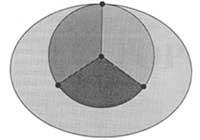
Noutras palabras, o que dicía a conxectura era que paira pintar todo mapa era necesario e suficiente con utilizar catro cores diferentes. A necesidade de utilizar as catro cores queda demostrada co mapa da figura 5. (Isto non significa que todos os mapas píntense sempre con catro cores. Paira pintar algúns mapas bastarán dous ou tres cores). A segunda parte, que era suficiente, foi até hai pouco máis difícil de demostrar.
Ano 1946 S. M. O matemático Backer demostrou a conxectura paira mapas de 35 ou menos poboacións. C. Appel e W. Haken, recentemente, en 1976, demostrou en colaboración mediante computaciones e métodos teóricos.
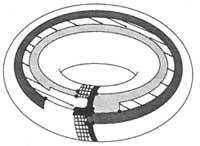
Tamén se expuxeron problemas similares. Por exemplo, foi máis fácil demostrar a conxectura das cinco cores. O problema das cores pódese expor noutras superficies pechadas ademais da esfera ou o plano. No caso do “touro”, por exemplo, necesítanse polo menos sete cores, tal e como o demostra o mapa da figura 6. Neste caso é fácil demostrar que as sete cores son suficientes.
Non debemos pensar que o único obxectivo da Topología é estudar ou resolver este tipo de curiosidades. Estes son só o escaparate dunha das ciencias máis profundas da actualidade. Ao mesmo tempo pódese dicir que os conceptos máis sinxelos da Topología son utilizados por moita xente que sabe o que é a Topología. Os conceptos básicos de topología son tan básicos que aprendemos de neno: interior, exterior, fronteira, dereita, esquerda, conexión, etc.
Paira finalizar, propómosche dous traballos. O primeiro consiste en analizar a solución do problema tras colocar a oitava ponte sobre o río Pregel da cidade de Koenigsberg, representado na figura 7. A segunda, tomando o mapa de Euskal Herria e debuxando os límites de todas as comarcas, tenta pintar coa menor cor posible.