Topología
En el número anterior mencionamos el área de Topología y decíamos que era una rama matemática que estudia las propiedades geométricas inmutables a los rizos y estiramientos.
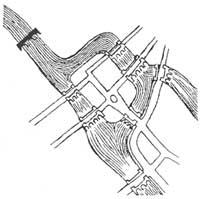
Un problema de Topología: ¿se puede convertir la cámara de un neumático (es decir, sacar el interior al exterior y meter el exterior al interior) sin cortar ni perforar la cámara?
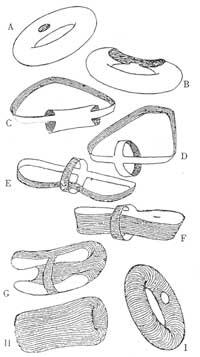
Mientras en la práctica tendríamos que decir que no, en Topología diremos que sí. Como hemos dicho en la Topología los objetos se pueden rizar y tirar como se quiera. Para darle la vuelta a la cámara hay que seguir las siguientes instrucciones (te recomendamos que no lo intentes con la cámara real): indicaremos que el orificio que aparece en la imagen es el lugar en el que se coloca la válvula; colocando un dedo en el agujero hay que extenderlo cada vez más (A,B) hasta que la cámara toma la forma de las dos bandas de goma unidas (C,D); cada tira da la vuelta a cada tira es la normal hasta que se da la parte externa. Ten en cuenta que la dirección de las estrías de la cámara ha cambiado. Si al principio estaban por la cámara, ahora se pueden ver en dirección perpendicular. Así que hemos dado la vuelta a la cámara. Las cámaras iniciales y finales en topología son iguales.
Este tipo de problemas son los que dan a la Topología la otra apariencia, ya que parecen enmascarar este nuevo campo de las Matemáticas. En el número 29 te hablamos de la cinta de Möbius y de la botella de Klein, los mejores juguetes de los topólogos.
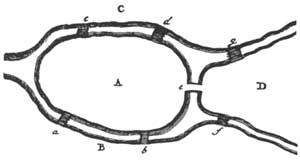
Desde un punto de vista histórico, Leibniz descubrió inicialmente este nuevo campo de las Matemáticas y lo denominó expresamente “Analysis Situs”. Más tarde se incorporó a la historia de la Topología el nombre de otro importante matemático, Leonhard Euler. La anécdota ya es conocida y XVIII. En el siglo XX se ubica en la ciudad de Koenigsberg. El río Pregel que pasa por esta ciudad era cruzado por siete puentes que unían las orillas del río con las dos islas (como se puede apreciar en la figura 2). A la gente de la zona le gustaba, desde hace tiempo, intentar pasar una sola vez por los siete puentes. A pesar de los ensayos y ensayos realizados, no encontraron solución al problema.
Cuando el problema llegó a manos de Euler en 1736, pronto se dio cuenta de que la solución no estaba en el cálculo de alguna medida. Y que no se podía resolver mediante cálculos cuantitativos. La posición de los territorios y puentes determina la naturaleza del problema. Sabía que si se probaran todas las posibilidades de cruzar los siete puentes, una a una, se podía dar una respuesta correcta, pero él no lo hizo. Por un lado era un método aburrido y por otro lado la solución no serviría para otros problemas.
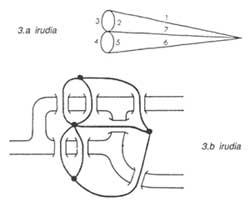
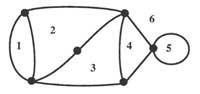
Vamos a sustituir, por ejemplo, los territorios por puntos y las líneas que unen los puentes dos puntos. Así obtenemos los gráficos de la figura 3. Puede pensarse que las distancias entre puntos o las longitudes de las vías no influyen en la resolución del problema. El planteamiento ahora sería el siguiente: los “grafos” o “redes” que se ven en la figura 3, sin que el bolígrafo se deslice de la página, deben hacerse sin pasar dos veces por cada vía.
En la solución ideada por Euler, tuvo en cuenta el número de puentes entre diferentes territorios. Puedes encontrar la solución adaptada en el número 13 de la revista Elhuyar.
Este problema es sin labios el ejemplo más famoso de la Teoría de Grafos. La Teoría de Grafos tiene sus raíces en el estudio de problemas de Topología que pueden describirse mediante los puntos denominados vértices y sus relaciones (esquinas). Euler dio relaciones entre el número de vértices, aristas y lados, siendo la diferencia la región en la que la red o el grafo divide la superficie. Dicha relación es nE + nA = ne + 2, nE = número de vértices, nA = número de lados y ne = número de bordes. Esta fórmula sirve para describir la relación entre el número de vértices, aristas y lados de un poliedro.
En la actualidad la Teoría de Grafos es independiente de la Topología y tiene numerosas aplicaciones fuera de las Matemáticas: Física teórica, Técnica, Teoría de la Red, etc.
Por la senda de los grafos podemos acercarnos a otro tema fascinante de la Topología, el “Problema de los cuatro colores”.
Cuando se imprimen mapas políticos, las estatuas contiguas se pintan con distintos colores. En la Topología o en la Teoría de Grafos se entiende por mapa la imagen formada por cantos, vértices y porciones generadas en la esfera o plano por un grafo de número finito de cantos. La zona conectada y los bordes que la delimitan (límites) se denominan Pueblos. (En la figura 5 se representan cuatro pueblos). Diremos que dos municipios son colindantes si tienen un borde común. Debes tomar los conceptos anteriores para que comprendamos bien la cuestión. El “problema de los cuatro colores” no era más que una conjetura y decía que todo mapa formado por conexiones populares, a pesar de su complejidad, se puede pintar en cuatro colores, en los que dos pueblos vecinos siempre toman dos colores diferentes.
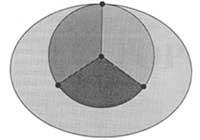
En otras palabras, lo que decía la conjetura era que para pintar todo mapa era necesario y suficiente con utilizar cuatro colores diferentes. La necesidad de utilizar los cuatro colores queda demostrada con el mapa de la figura 5. (Esto no significa que todos los mapas se pinten siempre con cuatro colores. Para pintar algunos mapas bastarán dos o tres colores). La segunda parte, que era suficiente, ha sido hasta hace poco más difícil de demostrar.
Año 1946 S. M. El matemático Backer demostró la conjetura para mapas de 35 o menos poblaciones. C. Appel y W. Haken, recientemente, en 1976, demostró en colaboración mediante computaciones y métodos teóricos.
También se han planteado problemas similares. Por ejemplo, ha sido más fácil demostrar la conjetura de los cinco colores. El problema de los colores se puede plantear en otras superficies cerradas además de la esfera o el plano. En el caso del “toro”, por ejemplo, se necesitan al menos siete colores, tal y como lo demuestra el mapa de la figura 6. En este caso es fácil demostrar que los siete colores son suficientes.
No debemos pensar que el único objetivo de la Topología es estudiar o resolver este tipo de curiosidades. Estos son sólo el escaparate de una de las ciencias más profundas de la actualidad. Al mismo tiempo se puede decir que los conceptos más sencillos de la Topología son utilizados por mucha gente que sabe lo que es la Topología. Los conceptos básicos de topología son tan básicos que aprendemos de niño: interior, exterior, frontera, derecha, izquierda, conexión, etc.
Para finalizar, te proponemos dos trabajos. El primero consiste en analizar la solución del problema tras colocar el octavo puente sobre el río Pregel de la ciudad de Koenigsberg, representado en la figura 7. La segunda, tomando el mapa de Euskal Herria y dibujando los límites de todas las comarcas, intenta pintar con el menor color posible.