Topologie
Dans le numéro précédent, nous avons mentionné le domaine de la topologie et avons dit qu'il était une branche mathématique qui étudie les propriétés géométriques immuables à des boucles et des étirements.
Un problème de topologie: Peut-on convertir la chambre d'un pneu (c'est-à-dire retirer l'intérieur à l'extérieur et mettre l'extérieur à l'intérieur) sans couper ni percer la caméra?
Alors que dans la pratique, nous devrions dire non, en Topologie, nous dirons oui. Comme nous l'avons dit dans la topologie, les objets peuvent être ridés et tirés comme vous le souhaitez. Pour retourner la caméra, il faut suivre les instructions suivantes (nous vous recommandons de ne pas l'essayer avec la caméra réelle): nous indiquerons que le trou qui apparaît dans l'image est l'endroit où la vanne est placée; en plaçant un doigt dans le trou, il faut l'étendre de plus en plus (A,B) jusqu'à ce que la caméra prend la forme des deux bandes de caoutchouc jointes (C,D); chaque bande externe donne la. Notez que la direction des vergetures de la caméra a changé. Si au début ils étaient par la caméra, ils peuvent maintenant être vus dans la direction perpendiculaire. Nous avons donc fait le tour de la caméra. Les caméras initiales et finales en topologie sont les mêmes.
Ce genre de problèmes sont ceux qui donnent à la topologie l'autre apparence, car ils semblent masquer ce nouveau domaine des mathématiques. Dans le numéro 29, nous vous parlons du ruban de Möbius et de la bouteille de Klein, les meilleurs jouets des topologues.
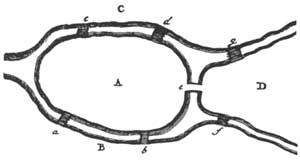
D'un point de vue historique, Leibniz a d'abord découvert ce nouveau domaine des mathématiques et l'a expressément nommé “Analysis Situs”. Plus tard, il a rejoint l'histoire de la topologie du nom d'un autre important mathématicien, Leonhard Euler. L'anecdote est déjà connue et XVIII. Au XXe siècle, il est situé dans la ville de Koenigsberg. Le fleuve Pregel qui traverse cette ville était traversé par sept ponts reliant les rives du fleuve aux deux îles (comme on peut le voir dans la figure 2). Les gens de la région aimaient, depuis longtemps, essayer de passer une seule fois sur les sept ponts. Malgré les essais et essais réalisés, ils n'ont trouvé aucune solution au problème.
Lorsque le problème est arrivé à Euler en 1736, il a vite réalisé que la solution n'était pas dans le calcul d'une mesure. Et il ne pouvait pas être résolu par des calculs quantitatifs. La position des territoires et des ponts détermine la nature du problème. Je savais que si toutes les possibilités de franchir les sept ponts étaient testées, l'une après l'autre, on pouvait donner une réponse correcte, mais il ne l'a pas fait. D'une part c'était une méthode ennuyeuse et d'autre part la solution ne servirait pas pour d'autres problèmes.
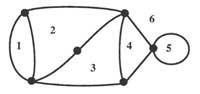
Nous allons remplacer, par exemple, les territoires par des points et les lignes qui relient les ponts deux points. Nous obtenons ainsi les graphiques de la figure 3. On peut penser que les distances entre les points ou les longueurs des voies n'influencent pas la résolution du problème. L'approche serait maintenant la suivante: les “graphes” ou “réseaux” que l'on voit dans la figure 3, sans que le stylo glisse de la page, doivent être faites sans passer deux fois par voie.
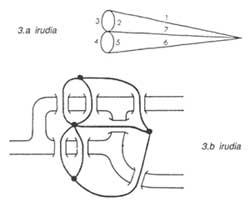
Dans la solution conçue par Euler, il a tenu compte du nombre de ponts entre les différents territoires. Vous pouvez trouver la solution adaptée dans le numéro 13 du magazine Elhuyar.
Ce problème est sans lèvres l'exemple le plus célèbre de la théorie des graphes. La théorie des graphes a ses racines dans l'étude des problèmes de topologie qui peuvent être décrits par les points appelés sommets et leurs relations (coins). Euler a donné des relations entre le nombre de sommets, arêtes et côtés, la différence étant la région dans laquelle le réseau ou le graphe divise la surface. Ce rapport est nE + nA = ne + 2, nE = nombre de sommets, nA = nombre de côtés et ne = nombre de bords. Cette formule sert à décrire la relation entre le nombre de sommets, arêtes et côtés d'un polyèdre.
Actuellement, la théorie des graphes est indépendante de la topologie et a de nombreuses applications en dehors des mathématiques: Physique théorique, technique, théorie du réseau, etc.
Sur le chemin des graphes, nous pouvons aborder un autre sujet fascinant de la topologie, le “Problème des quatre couleurs”.
Lorsque des cartes politiques sont imprimées, les statues adjacentes sont peintes en différentes couleurs. Dans la Topologie ou dans la Théorie des Graphes on entend par carte l'image formée par des chants, des sommets et des portions générés dans la sphère ou plan par un graphe de nombre fini de chants. La zone connectée et les bords qui la délimitent (limites) sont appelés Villages. (La figure 5 représente quatre peuples). Nous dirons que deux municipalités sont adjacentes si elles ont un bord commun. Vous devez prendre les concepts ci-dessus pour bien comprendre la question. Le “problème des quatre couleurs” n’était qu’une conjecture et disait que toute carte formée de connexions populaires, malgré sa complexité, peut être peinte en quatre couleurs, dans lesquelles deux villages voisins prennent toujours deux couleurs différentes.
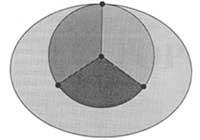
En d'autres termes, ce que disait la conjecture était que pour peindre toute carte il était nécessaire et suffisant d'utiliser quatre couleurs différentes. La nécessité d'utiliser les quatre couleurs est démontrée avec la carte de la figure 5. (Cela ne signifie pas que toutes les cartes sont toujours peintes avec quatre couleurs. Pour peindre quelques cartes, il suffit de deux ou trois couleurs). La deuxième partie, qui était suffisante, a été jusqu'à récemment plus difficile à démontrer.
Année 1946 S. M. Le mathématicien Backer a montré la conjecture pour des cartes de 35 ou moins populations. C. Appel et W. Haken, récemment, en 1976, a démontré en collaboration par des calculs et des méthodes théoriques.
Des problèmes similaires ont également été soulevés. Par exemple, il a été plus facile de démontrer la conjecture des cinq couleurs. Le problème des couleurs peut être posé sur d'autres surfaces fermées en plus du cadran ou du plan. Dans le cas du taureau, par exemple, il faut au moins sept couleurs, comme le montre la carte de la figure 6. Dans ce cas, il est facile de prouver que les sept couleurs sont suffisantes.
Nous ne devons pas penser que le seul but de la topologie est d'étudier ou de résoudre ce type de curiosités. Ce ne sont que la vitrine de l'une des sciences les plus profondes de l'actualité. En même temps, on peut dire que les concepts les plus simples de la topologie sont utilisés par beaucoup de gens qui savent ce qu'est la topologie. Les bases de la topologie sont si élémentaires que nous apprenons de l'enfant: intérieur, extérieur, frontière, droite, gauche, connexion, etc.
Pour terminer, nous vous proposons deux travaux. Le premier consiste à analyser la solution du problème après avoir placé le huitième pont sur le fleuve Pregel de la ville de Koenigsberg, représenté sur la figure 7. La seconde, en prenant la carte d'Euskal Herria et en dessinant les limites de toutes les régions, essaie de peindre avec la moindre couleur possible.