Topology of topology
In the previous issue we mentioned the area of Topology and said it was a mathematical branch that studies the unchanging geometric properties to curls and stretches.
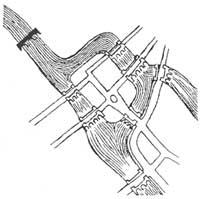
A problem of Topology: Can the camera of a tyre be converted (that is, pull the inside out and put the outside inside) without cutting or drilling the camera?
While in practice we would have to say no, in Topology we will say yes. As we have said in the Topology, objects can be ridged and thrown as desired. To turn the camera around you have to follow the instructions below (we recommend that you do not try it with the actual camera): we will indicate that the hole that appears in the image is the place where the valve is placed; by placing a finger in the hole you have to extend it more and more (A,B) until the camera takes the shape of the two rubber bands attached (C,D); each gives the normal part. Note that the direction of the camera's striations has changed. If at first they were in the camera, now they can be seen in a perpendicular direction. So we have turned the camera around. The initial and final cameras in topology are the same.
This type of problems are those which give Topology the other appearance, since they seem to mask this new field of Mathematics. In number 29 we talk about the tape of Möbius and the bottle of Klein, the best toys of the topologists.
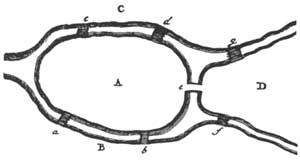
From a historical point of view, Leibniz initially discovered this new field of mathematics and expressly called it “Analysis Situs”. Later he incorporated into the history of Topology the name of another important mathematician, Leonhard Euler. The anecdote is already known and XVIII. In the twentieth century it is located in the city of Koenigsberg. The Pregel river that passes through this city was crossed by seven bridges linking the banks of the river with the two islands (as can be seen in figure 2). People in the area liked, for a long time, trying to pass through the seven bridges only once. Despite the trials and trials carried out, they found no solution to the problem.
When the problem came to Euler's hands in 1736, he soon realized that the solution was not in the calculation of some measure. And that could not be solved by quantitative calculations. The position of territories and bridges determines the nature of the problem. He knew that if all the possibilities of crossing the seven bridges were tested, one by one, a correct answer could be given, but he did not. On the one hand it was a boring method and on the other hand the solution would not serve for other problems.
Let's replace, for example, the territories by points and the lines that link the bridges two points. Thus we get the graphics of figure 3. It can be thought that the distances between points or the lengths of the tracks do not influence the resolution of the problem. The approach would now be as follows: the “graphs” or “networks” shown in figure 3, without the pen slipping from the page, must be done without passing twice by each way.
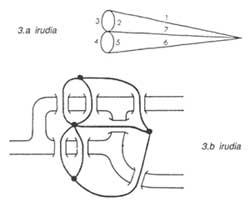
In the solution devised by Euler, he took into account the number of bridges between different territories. You can find the solution adapted in number 13 of the magazine Elhuyar.
This problem is without lips the most famous example of the Graph Theory. Graph Theory has its roots in the study of Topology problems that can be described by points called vertices and their relationships (corners). Euler gave relationships between the number of vertices, edges and sides, being the difference the region in which the network or graph divides the surface. This relationship is nE + nA = ne + 2, nE = number of vertices, nA = number of sides and ne = number of edges. This formula serves to describe the relationship between the number of vertices, edges and sides of a polyhedron.
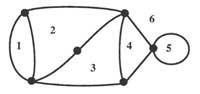
Currently the Graph Theory is independent of Topology and has numerous applications outside of Mathematics: Theoretical physics, Technique, Network Theory, etc.
On the path of the graphs we can approach another fascinating theme of the Topology, the “Problem of the four colors”.
When political maps are printed, the adjacent statues are painted in different colours. In the Topology or in the Theory of Graphs the image formed by songs, vertices and portions generated in the sphere or plane by a graph of finite number of songs is understood by map. The connected zone and the edges that define it (limits) are called Villages. (Figure 5 shows four villages). We will say that two municipalities are adjacent if they have a common edge. You must take the above concepts so that we understand the question well. The “problem of the four colors” was nothing more than a conjecture and said that every map formed by popular connections, despite its complexity, can be painted in four colors, in which two neighboring villages always take two different colors.
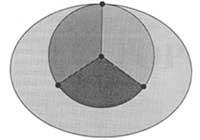
In other words, what the conjecture said was that to paint all map it was necessary and enough to use four different colors. The need to use the four colors is demonstrated with the map of figure 5. (This does not mean that all maps are always painted in four colors. To paint some maps, two or three colors will suffice). The second part, which was enough, has been until a little more difficult to prove.
Year 1946 S. M. M. The mathematician Backer showed the conjecture for maps of 35 or fewer populations. C. C. Appel and W. Haken, recently, in 1976, demonstrated in collaboration through computations and theoretical methods.
Similar problems have also been raised. For example, it has been easier to demonstrate the conjecture of the five colors. The problem of colors can be raised on other closed surfaces in addition to the sphere or plane. In the case of the “bull”, for example, at least seven colors are needed, as shown in figure 6. In this case it is easy to show that the seven colors are sufficient.
We should not think that the only objective of Topology is to study or solve this kind of curiosities. These are only the showcase of one of the deepest sciences of today. At the same time it can be said that the simplest concepts of Topology are used by many people who know what Topology is. The basic concepts of topology are so basic that we learn from child: interior, exterior, border, right, left, connection, etc.
To finish, we propose two works. The first consists of analyzing the solution of the problem after placing the eighth bridge over the Pregel river of the city of Koenigsberg, represented in figure 7. The second, taking the map of Euskal Herria and drawing the limits of all the regions, tries to paint with the least color possible.