Topologia
En el número anterior esmentem l'àrea de Topologia i dèiem que era una branca matemàtica que estudia les propietats geomètriques immutables als rínxols i estiraments.
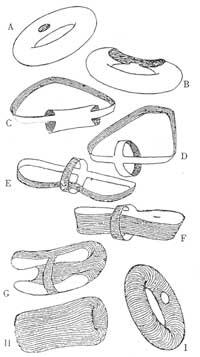
Un problema de Topologia: es pot convertir la cambra d'un pneumàtic (és a dir, treure l'interior a l'exterior i ficar l'exterior a l'interior) sense tallar ni perforar la cambra?
Mentre en la pràctica hauríem de dir que no, en Topologia direm que sí. Com hem dit en la Topologia els objectes es poden arrissar i tirar com es vulgui. Per a donar-li la volta a la cambra cal seguir les següents instruccions (et recomanem que no ho intentis amb la cambra real): indicarem que l'orifici que apareix en la imatge és el lloc en el qual es col·loca la vàlvula; col·locant un dit en el forat cal estendre'l cada vegada més (A,B) fins que la cambra pren la forma de les dues bandes de goma unides (C,D); cada tira dóna la volta a cada tira és la normal fins que es dóna la part externa. Tingues en compte que la direcció de les estries de la cambra ha canviat. Si al principi estaven per la cambra, ara es poden veure en direcció perpendicular. Així que hem donat la volta a la cambra. Les cambres inicials i finals en topologia són iguals.
Aquest tipus de problemes són els que donen a la Topologia l'altra aparença, ja que semblen emmascarar aquest nou camp de les Matemàtiques. En el número 29 et parlem de la cinta de Möbius i de l'ampolla de Klein, les millors joguines dels topólogos.
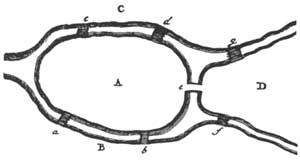
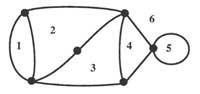
Des d'un punt de vista històric, Leibniz va descobrir inicialment aquest nou camp de les Matemàtiques i el va denominar expressament “Analysis Situs”. Més tard es va incorporar a la història de la Topologia el nom d'un altre important matemàtic, Leonhard Euler. L'anècdota ja és coneguda i XVIII. En el segle XX se situa a la ciutat de Koenigsberg. El riu Pregel que passa per aquesta ciutat era creuat per set ponts que unien les ribes del riu amb les dues illes (com es pot apreciar en la figura 2). A la gent de la zona li agradava, des de fa temps, intentar passar una sola vegada pels set ponts. Malgrat els assajos i assajos realitzats, no van trobar solució al problema.
Quan el problema va arribar a les mans d'Euler en 1736, aviat es va adonar que la solució no estava en el càlcul d'alguna mesura. I que no es podia resoldre mitjançant càlculs quantitatius. La posició dels territoris i ponts determina la naturalesa del problema. Sabia que si es provessin totes les possibilitats de creuar els set ponts, una a una, es podia donar una resposta correcta, però ell no ho va fer. D'una banda era un mètode avorrit i d'altra banda la solució no serviria per a altres problemes.
Substituirem, per exemple, els territoris per punts i les línies que uneixen els ponts dos punts. Així obtenim els gràfics de la figura 3. Pot pensar-se que les distàncies entre punts o les longituds de les vies no influeixen en la resolució del problema. El plantejament ara seria el següent: els “grafs” o “xarxes” que es veuen en la figura 3, sense que el bolígraf es llisqui de la pàgina, han de fer-se sense passar dues vegades per cada via.
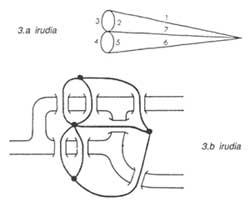
En la solució ideada per Euler, va tenir en compte el nombre de ponts entre diferents territoris. Pots trobar la solució adaptada en el número 13 de la revista Elhuyar.
Aquest problema és sense llavis l'exemple més famós de la Teoria de Grafs. La Teoria de Grafs té les seves arrels en l'estudi de problemes de Topologia que poden descriure's mitjançant els punts denominats vèrtexs i les seves relacions (cantonades). Euler va donar relacions entre el nombre de vèrtexs, arestes i costats, sent la diferència la regió en la qual la xarxa o el graf divideix la superfície. Aquesta relació és nE + nA = ne + 2, nE = nombre de vèrtexs, nA = nombre de costats i ne = nombre de vores. Aquesta fórmula serveix per a descriure la relació entre el nombre de vèrtexs, arestes i costats d'un poliedre.
En l'actualitat la Teoria de Grafs és independent de la Topologia i té nombroses aplicacions fora de les Matemàtiques: Física teòrica, Tècnica, Teoria de la Xarxa, etc.
Per la senda dels grafs podem acostar-nos a un altre tema fascinant de la Topologia, el “Problema dels quatre colors”.
Quan s'imprimeixen mapes polítics, les estàtues contigües es pinten amb diferents colors. En la Topologia o en la Teoria de Grafs s'entén per mapa la imatge formada per cants, vèrtexs i porcions generades en l'esfera o pla per un graf de nombre finit de cants. La zona connectada i les vores que la delimiten (límits) es denominen Pobles. (En la figura 5 es representen quatre pobles). Direm que dos municipis són confrontants si tenen una vora comuna. Has de prendre els conceptes anteriors perquè comprenguem bé la qüestió. El “problema dels quatre colors” no era més que una conjectura i deia que tot mapa format per connexions populars, malgrat la seva complexitat, es pot pintar en quatre colors, en els quals dos pobles veïns sempre prenen dos colors diferents.
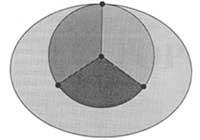
En altres paraules, el que deia la conjectura era que per a pintar tot mapa era necessari i suficient amb utilitzar quatre colors diferents. La necessitat d'utilitzar els quatre colors queda demostrada amb el mapa de la figura 5. (Això no significa que tots els mapes es pintin sempre amb quatre colors. Per a pintar alguns mapes bastaran dos o tres colors). La segona part, que era suficient, ha estat fins fa poc més difícil de demostrar.
Any 1946 S. M. El matemàtic Backer va demostrar la conjectura per a mapes de 35 o menys poblacions. C. Appel i W. Haken, recentment, en 1976, va demostrar en col·laboració mitjançant computacions i mètodes teòrics.
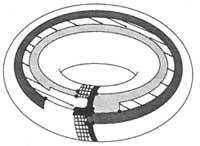
També s'han plantejat problemes similars. Per exemple, ha estat més fàcil demostrar la conjectura dels cinc colors. El problema dels colors es pot plantejar en altres superfícies tancades a més de l'esfera o el pla. En el cas del “toro”, per exemple, es necessiten almenys set colors, tal com el demostra el mapa de la figura 6. En aquest cas és fàcil demostrar que els set colors són suficients.
No hem de pensar que l'únic objectiu de la Topologia és estudiar o resoldre aquest tipus de curiositats. Aquests són només l'aparador d'una de les ciències més profundes de l'actualitat. Al mateix temps es pot dir que els conceptes més senzills de la Topologia són utilitzats per molta gent que sap el que és la Topologia. Els conceptes bàsics de topologia són tan bàsics que aprenem de nen: interior, exterior, davantera, dreta, esquerra, connexió, etc.
Per a finalitzar, et proposem dos treballs. El primer consisteix a analitzar la solució del problema després de col·locar el vuitè pont sobre el riu Pregel de la ciutat de Koenigsberg, representat en la figura 7. La segona, prenent el mapa d'Euskal Herria i dibuixant els límits de totes les comarques, intenta pintar amb el menor color possible.