Topologia
Aurreko alean Topologi arloa aipatu genuen, eta zera genion: kizkurpen eta teinkadekiko aldaezin matentzen diren propietate geometrikoak aztertzen dituen matematika-adarra zela.
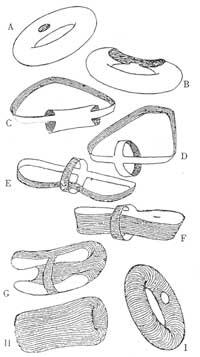
Hona hemen Topologiako problema bat: bihur al daiteke pneumatiko baten kamara (hots, barne aldea kanpora atera eta kanpo aldea barrura sartu) kamara ebaki edo zulatu gabe?
Praktikan ezetz esan beharko genukeen bitartean, Topologian baietz esango dugu zalantzarik gabe. Esan dugunez Topologian objektuak nahi den bezala kizkur eta tira daitezke. Kamarari buelta emateko, ondoko argibideei jarraitu behar zaie (benetako kamararekin ez saiatzea gomendatzen dizugu): irudian dagoen zuloa balbula kokatzen den lekua dela esan behar dugu; hatzamar bat zuloan ipiniz zuloa gero eta gehiago zabaldu behar da (A,B) kamarak gomazko bi zerrenda lotuen itxura (C,D) hartu arte; zerrenda bakoitzari buelta erdia ematen zaio (E); honek kamarari buelta ematen dio, barne aldea kanporatuz eta kanpo aldea barneratuz; hurrengo pausua gomazko zerrendak tiratzean datza, kamararen itxura arrunta lortu arte (F, G, H, I). Kontura zaitez kamararen ildasken norabidea aldatu egin dela. Hasieran kamaran zehar bazeuden, orain norabide perpendikularrean ikus daitezke. Hortaz kamarari buelta eman diogu. Topologian hasierako eta bukaerako kamarak berdinak dira.
Honelako problemek ematen diote beste itxura Topologiari; bitxikeri itxuraz maskaratzen bait dute Matematikaren arlo berri hau. 29. alean Möbius-en xingolaz eta Klein-en botilaz mintzatu gintzaizkizun; topologoen jostailurik ederrenez.
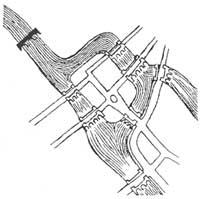
Historiari pixka bat begiratuta, hasiera batean Leibniz-ek atzeman zuen Matematikaren arlo berri hau eta “Analysis Situs” espresioz izendatu zuen. Geroago beste matematikari ospetsu baten izena sartu zen Topologiaren historiara; Leonhard Euler hain zuzen. Pasadizoa ezaguna da jadanik eta XVIII. mendean Koenigsberg hirian kokatzen da. Hiri honetatik igarotzen den Pregel ibaia zazpi zubik gurutzatzen zuten, ibaiaren ertzak eta bi irlak lotzen zituztelarik (2. irudian ikusten den bezala). Bertako jendeak gustokoa zuen, aspalditik, zazpi zubietatik behin bakarrik pasatzen saiatzea. Saioak eta saioak egin bazituzten ere, problemari ez zioten soluziorik aurkitu.
Problema 1736. urtean Eulerren eskuetara heldu zenean, berehala ohartu zen soluzioa ez zetzala neurriren baten kalkuluan. Eta kalkulu kuantitatiboen bidez ezin zela ebatzi ere bai. Izan ere, lurraldeen eta zubien posizioak problemaren izaera determinatzen bait du. Bazekien, zazpi zubiak gurutzatzeko posibilitate guztiak banan-banan probatuz gero erantzun zuzena eman zitekeela ere, baina berak ez zuen hortik jo. Alde batetik metodo aspergarria bait zen eta bestalde soluzioak ez bait zukeen beste problema ezberdinetarako balioko.
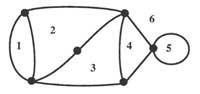
Ordezka ditzagun, esaterako, lurraldeak puntuen bidez eta zubiak bi puntu lotzen dituzten lerroen bidez. Honela 3. irudiko grafikoak lortuko ditugu. Pentsa daitekeenez, puntuen arteko distantziek edo bideen luzerek ez dute eraginik problemaren ebazpenean. Orain planteamendua hauxe litzateke: hirugarren irudian ikusten diren “grafoak” edo “sareak”, boligrafoa orritik altzatu gabe, egin behar dira bide bakoitzetik bi aldiz pasatu gabe.
Eulerrek asmatu zuen soluzioan, lurralde desberdinen arteko zubi-kopurua hartu zuen kontutan. Elhuyar aldizkariaren 13. alean aurki dezakezu soluzio egokitua.
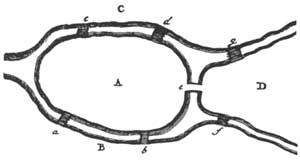
Problema hau da ezpairik gabe Grafo-Teoriaren adibiderik ospetsuena. Grafo-Teoriak erpin deituriko puntuen eta hauen arteko loturen (ertzen) bidez deskriba daitezkeen Topologiako problemen azterketan ditu sustraiak. Eulerrek erpin, ertz eta aldeen kopuruen arteko erlazioak eman zituen, aldea sareak edo grafoak gainazala zatitzen duen eskualdea izanik. Esandako erlazioa nE + nA = ne + 2 da, nE = erpin-kopurua, nA = alde-kopurua eta ne = ertz-kopurua direlarik. Formula honek poliedro baten erpin, ertz eta aldeen kopuruen arteko erlazioa deskribatzeko balio du.
Gaur egun Grafo-Teoria independentea da Topologiarekiko, eta aplikazio ugari dauka Matematika hutsetik at: Fisika teorikoa, Teknika, Sare-Teoria, etab.
Grafoen bidetik Topologiako beste auzi liluragarri batera hurbil gaitezke; “Lau koloreen problema” izeneko auzira hain zuzen.
Mapa politikoak inprimatzen direnean, ondoz ondoko estatuak kolore ezberdinez pintatzen dira. Topologian edo Grafo-Teorian mapatzat zera ulertu behar da: ertz-kopuru finituko grafo batek, esferan edo planoan sortutako eta ertzez, erpinez eta aldez osaturiko irudia. Alde konexuak eta bera mugatzen duten ertzek (mugak) Herri izena dute. (5. irudian lau herri daude). Bi herri aldamenekoak direla esango dugu ertz bat amankomuna badaukate. Aurreko kontzeptuak hartu behar dituzu auzia ongi uler dezagun. “Lau koloreen problema” izeneko auzia aieru bat besterik ez zen eta zera zioen: herri konexuz osaturiko mapa oro, oso korapilatsua bada ere, lau kolorez pinta daiteke, aldameneko bi herrik beti bi kolore ezberdin hartzen dituztelarik.
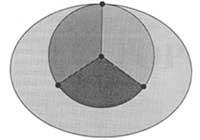
Beste hitzetan, aieruak esaten zuena zera zen: mapa oro pintatzeko beharrezkoa eta nahikoa zela lau kolore ezberdin erabiltzea. Lau koloreak erabiltzea beharrezkoa dela bostgarren irudiko maparekin geratzen da frogaturik. (Honek ez du esan nahi mapa guztiak pintatzeko beti lau kolore beharrezko direnik. Mapa batzuk pintatzeko nahikoa izango dira bi edo hiru kolore bakarrik). Bigarren zatia, nahikoa zela alegia, frogatzea zailagoa izan da duela gutxi arte.
1946. urtean S. M. Backer matematikariak frogatu zuen aierua 35 edo herri gutxiagoko mapetarako. K. Appel eta W. Haken-ek duela gutxi, 1976. urtean, frogatu zuten elkarlanean konputazio eta metodo teorikoen bidez.
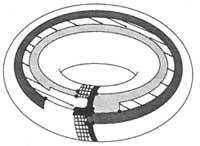
Antzeko problemak ere planteatu dira. Esate baterako, bost koloreen aierua frogatzea errazagoa suertatu da. Koloreen problema esfera edo planoz gain beste gainazal itxitan ere plantea daiteke. “Toru”an adibidez, gutxienez zazpi kolore behar dira, 6. irudiko mapak frogatzen duen bezala. Kasu honetan zazpi koloreak aski direla frogatzea ere erraza da.
Ez dugu pentsatu behar Topologiaren helburu bakarra honelako bitxikeriak aztertzea edo ebaztea denik. Hauek gaur egungo zientzia sakonenetako baten erakusleihoa besterik ez dira. Aldi berean esan daiteke Topologiako kontzepturik errazenak Topologia zer denez dakien jende askok erabiltzen dituela. Topologiako oinarrizko kontzeptuak hain oinarrizkoak dira, ezen umetan ikasten bait ditugu: barne aldea, kanpo aldea, muga, eskuina, ezkerra, konexutasuna, etab.
Bukatzeko, bi lan proposatuko dizkizugu. Lehenengoa 7. irudian agertzen den Koenigsberg hiriko Pregel ibai gainean zortzigarren zubia jarri eta gero, problemak soluziorik daukan aztertzean datza. Bigarrena Euskal Herriko mapa hartu eta eskualde guztien mugak marraztutakoan saia zaitez ahalik eta kolore gutxien erabiliz pintatzen.