Sundial (and II) Construction of sundial
To begin with, we must take into account the basic principles of sunwatches. The first is that the gnomon is twisted, that is, forming an angle of local latitude with the horizontal. The second, parallel to the North-South axis, directed to the North Pole. With this base, the quadrant that draws the plane in which the shadow and time lines are projected can be adapted in many ways. However, depending on it we will have different types of sundials.
The classic sundials are equatorial, horizontal, vertical meridiana or declining and lateral. The last three are placed on the walls of the buildings, the gnomon being a metal stick that protrudes from the wall. The first two have no canes and are merely decorative. In these latter cases the gnomon is usually a triangle and the shadow of a vertex marks the time.
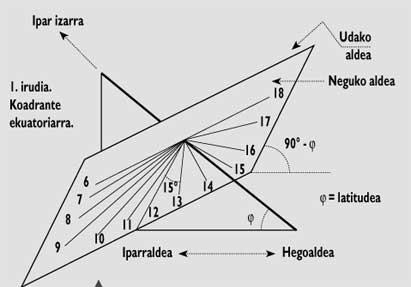
As mentioned in the previous article, sundials mark the real time of the sun. Thus, the noon of the sun (12) occurs when the Sun is in the South, that is, when the sun reaches its maximum height a day. Since the day has 24 hours and we can represent the way of the Sun through a circle, every twenty (15 degrees) corresponds an hour.
Thus, the line of 12 will be with the quadrant section plane of the vertical plane of the gnomon. Following this, the other lines can be drawn in equatorial quadrant forming angles of 15º compared to the previous one, plane perpendicular to gnomon and therefore parallel to the equator.
The construction of the equatorial quadrant is simple (Figure 1), but to be useful throughout the year it must have two faces or faces. At the top the shade will be projected in Spring-summer and at the bottom in Autumn-Winter. Keep in mind that the days of Equinox will not “work.”
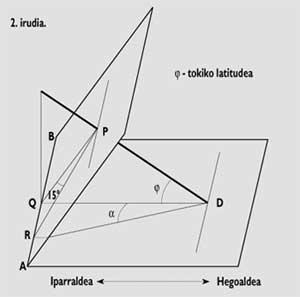
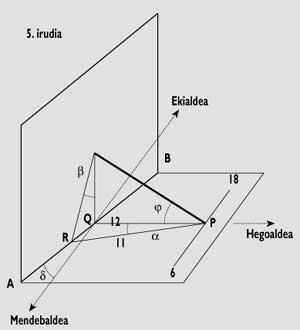
In all other cases, the angles to be different. These angles are formed by each time line at noon and can be calculated using trigonometric or geometric methods using QR distances (see figure 2).
To draw the time lines in a horizontal quadrant or in a vertical quadrant directed to the South, the end of these lines (points Q, R) will be taken as reference. These two points will match the equatorial block lines in line AB.
Trigonometry allows the resolution of angles:

Triangle QRD,
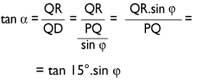
Therefore,
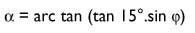
Instead of 15º, 30º, 45º, 60º, etc. If we put it, we will calculate the angles for 10, 9, 8.
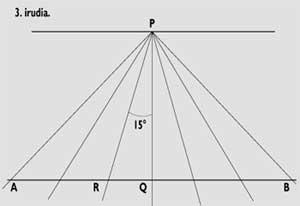
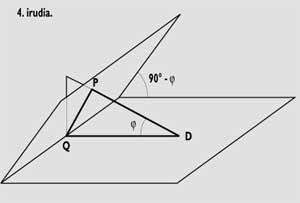
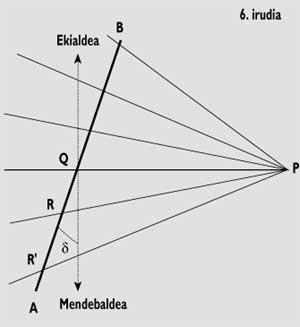
We can also do this without using trigonometric formulas. In this case, we must follow the steps detailed below. On the one hand, we built the gnomon and drew the midday line; then, we drew on a paper the equatorial quadrant (see figure 3) and in it we represented the line AB (perpendicular to the midday) where it would cut the plane of our clock. Here we will measure the distances between each time line (R) and the midday line (Q). We take these distances to our quadrant and connect them with the end of the gnomon. To represent the line AB of the equatorial quadrant, we will draw in another paper the right triangle PQD and measure the distances PQ and QD with a rule (see figure 4).
The construction of a vertical quadrant is similar. We continue to use the formulas we have used to create the horizontal quadrant with a single modification. That is, we replace the latitude with the coloration 90º-j (sen by cos).
Most sundials are vertical declining, as the walls totally south facing are not easy to find. The construction of these watches is more normal than the previous ones, so asymmetric time lines are obtained. To begin with, we must define the decline of the wall (diversion from the wall to the South). To do this we must represent the meridiana line, which is made using lead on a horizontal surface and the conveyor.
To draw the time lines we will follow the same previous system but starting with the horizontal quadrant that would have the same gnomon (see figure 5). Using trigonometry we obtain the following formula.
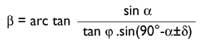
It is the angle we have calculated in the horizontal quadrant and the double sign of (+/-) determines the hours before and after 12.
If you want to discard all these formulas, you should draw the corresponding horizontal quadrant (see figure 6). It represents the line AB cutting of the two quadrants according to the declination of the wall and the distance PQ, to later measure distances QR, QR’, ...
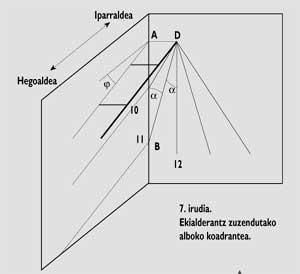
In the case of side clocks, that is, when the sundial is vertical or oriented to the East or to the West, we will place the gnomon parallel to the wall and the time lines will be parallel (see figure 7).
The distance between time lines is calculated from a theoretical quadrant. As in the previous case, AB distances should be measured in the edge section between gnomon and time lines. The trigonometric method to follow is simple: ABD in triangle in AB= AD.
On the other hand, sundials can not only indicate the time but also the date, for which we must analyze the shadow that generates the edge of the gnomon. In the case of ecuadorians, the calendar lines are concentric circles, which in the vertical and horizontal ones are conical (in our latitude, hyperbolas). The difficulty of drawing these curves can be avoided if you act in a practical way, that is, by marking the different positions of the edge of the gnomon throughout the day.