Rellotges de sol (i II) Construcció de rellotges de sol
Per a començar, hem de tenir en compte els principis bàsics dels rellotges de sol. La primera és que el gnòmon estigui tort, és a dir, formant un angle de latitud local amb l'horitzontal. El segon, paral·lel a l'eix Nord-Sud, dirigit al Pol Nord. Amb aquesta base, el quadrant que dibuixa el pla en el qual es projecta l'ombra i les línies horàries es pot adaptar de moltes maneres. No obstant això, depenent d'això tindrem diferents tipus de rellotges de sol.
Els rellotges de sol clàssics són equatorial, horitzontal, vertical meridiana o declinant i lateral. Les tres últimes es col·loquen en els murs dels edificis, sent el gnòmon un bastó metàl·lic que sobresurt del mur. Els dos primers no tenen bastons i són merament decoratius. En aquests últims casos la gnomona sol ser un triangle i l'ombra d'un vèrtex marca l'hora.
Com ja esmentem en l'article anterior, els rellotges de sol marquen l'hora real del sol. Així, el migdia del sol (12) es produeix quan el Sol està al Sud, és a dir, quan el sol aconsegueix la seva màxima altura al dia. Com el dia té 24 hores i podem representar el camí del Sol a través d'una circumferència, a cada vint (15 graus) correspon una hora.
Així, la línia de 12 serà amb el pla de secció quadrant del pla vertical del gnòmon. Seguint això, les altres línies es poden dibuixar en quadrant equatorial formant angles de 15° respecte a l'anterior, pla perpendicular a gnòmon i per tant paral·lel a l'equador.
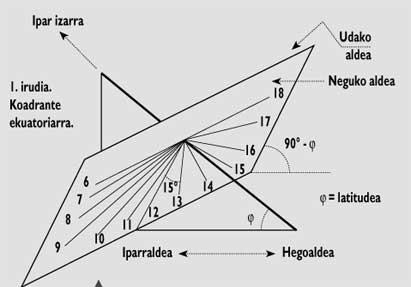
La construcció del quadrant equatorial és senzilla (Figura 1), però perquè sigui útil durant tot l'any ha de tenir dues cares o cares. En la part superior es projectarà l'ombra a la primavera-estiu i en la inferior a la tardor-Hivern. Tingues en compte que els dies d'Equinoccio no “funcionarà”.
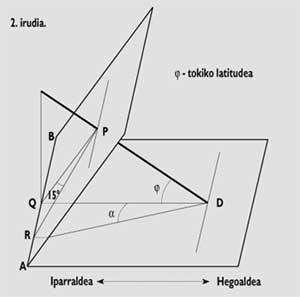
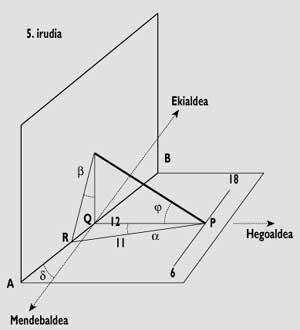
En tots els altres casos, els angles a seran diferents. Aquests angles es formen per cada línia horària al migdia i poden calcular-se mitjançant mètodes trigonomètrics o geomètrics utilitzant distàncies QR (veure figura 2).
Per a dibuixar les línies horàries en un quadrant horitzontal o en un quadrant vertical dirigit al Sud, es prendrà com a referència l'extrem d'aquestes línies (punts Q, R). Aquests dos punts coincidiran amb les línies del cuadrate equatorial en la línia AB.
La trigonometria permet la resolució d'angles:

Triangle QRD,
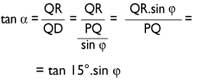
Per tant,
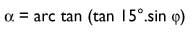
En lloc de 15°, 30°, 45°, 60°, etc. Si ho posem, calcularem els angles per a 10, 9, 8.
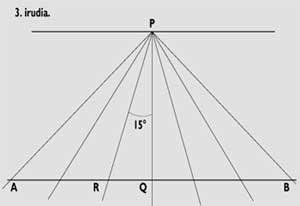
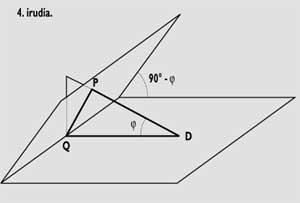
També podem fer-ho sense utilitzar fórmules trigonomètriques. En aquest cas, haurem de seguir els passos que es detallen a continuació. D'una banda, construïm el gnòmon i dibuixem la línia del migdia; després, dibuixem en un paper el quadrant equatorial (veure figura 3) i en ell representem la línia AB (perpendicular al migdia) on tallaria el pla del nostre rellotge. Aquí mesurarem les distàncies entre cada línia horària (R) i la línia del migdia (Q). Aquestes distàncies les portem al nostre quadrant i les unirem amb l'extrem del gnòmon. Per a representar la línia AB del quadrant equatorial, dibuixarem en un altre paper el triangle recte PQD i mesurarem les distàncies PQ i QD amb una regla (veure figura 4).
La construcció d'un quadrant vertical és similar. Es continuen utilitzant les fórmules que hem utilitzat per a crear el quadrant horitzontal amb una única modificació. És a dir, substituïm la latitud per la colatitud 90°-j (sen per cos ).
La majoria dels rellotges de sol són verticals declinants, ja que els murs totalment orientats al Sud no són fàcils de trobar. La construcció d'aquests rellotges és més normal que les anteriors, per la qual cosa s'obtenen línies horàries asimètriques. Per a començar, cal definir la declinació del mur (desviament del mur al Sud). Per a això cal representar la línia meridiana, que es realitza utilitzant el plom en una superfície horitzontal i el transportador.
Per a dibuixar les línies horàries seguirem el mateix sistema anterior però començant pel quadrant horitzontal que tindria el mateix gnòmon (veure figura 5). Utilitzant la trigonometria obtenim la següent fórmula.
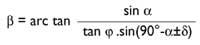
És l'angle que hem calculat en el quadrant horitzontal i el signe doble de (+/-) determina les hores anterior i posterior a les 12.
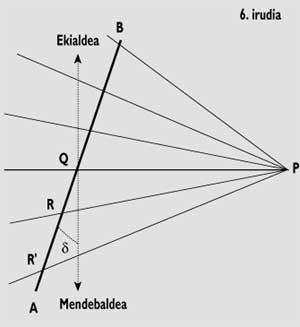
Si es volen descartar totes aquestes fórmules s'haurà de dibuixar el quadrant horitzontal corresponent (veure figura 6). En ell es representa la línia AB tallant dels dos quadrants en funció de la declinació del mur i la distància PQ, per a posteriorment mesurar distàncies QR, QR’, ...
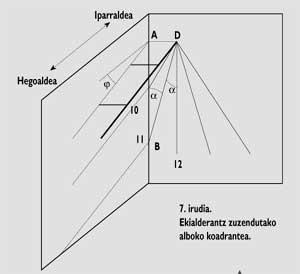
En el cas dels rellotges laterals, és a dir, quan el rellotge de sol és vertical o està orientat cap a l'Est o cap a l'Oest, col·locarem la gnomona paral·lela a la paret i les línies horàries seran paral·leles (veure figura 7).
La distància entre les línies horàries es calcula a partir d'un quadrant teòric. Com en el cas anterior, les distàncies AB han de mesurar-se en la secció de la vora entre el gnòmon i les línies horàries. El mètode trigonomètric a seguir és senzill: ABD en triangle en AB= AD.
D'altra banda, els rellotges de sol no sols poden indicar l'hora sinó també la data, per a això hem d'analitzar l'ombra que genera la vora del gnòmon. En el cas dels equatorials, les línies de calendari són circumferències concèntriques, que en les verticals i horitzontals són còniques (en la nostra latitud, hiperbolas). La dificultat de dibuixar aquestes corbes es pot evitar si s'actua de manera pràctica, és a dir, marcant al llarg del dia les diferents posicions de la vora del gnòmon.