Problemas matemáticos fáciles de entender pero difíciles de resolver
Os matemáticos investigan problemas de enxeñaría, bioloxía, etc. E é que grazas a demostracións baseadas nas matemáticas, podemos entender o comportamento dos fenómenos que se producen no mundo e na natureza.
Ás veces, os problemas que se estudan en matemáticas están compostos por ecuacións xigantes, polo que moita xente cre que son moi difíciles de resolver. Outros problemas son moi fáciles de entender (en moitos casos poden aparecer nunha liña), pero os matemáticos pasaron anos buscando a súa demostración. Por tanto, podemos dicir que son moi difíciles de resolver. Neste artigo falaremos sobre problemas matemáticos facilmente explicables (e mesmo comprensibles) pero difíciles de demostrar.
Deixade que explique que é resolver un problema matemático. Supoñamos que queremos resolver o problema denominado X. Como se fai? Paira demostrar que X é falsa basta con atopar un exemplo. Por exemplo, consideremos o problema: ''todos os números son normais''. Paira demostrar que isto é falso hai que dar un número que non sexa normal, por exemplo 3/2. Con iso podemos concluír que non todos os números son normais. Pero paira concluír que X é certo necesitamos una demostración. Consideremos o problema: ''a suma das cifras de todos os números divisibles por tres pódese dividir por tres''. Por exemplo, o número 12 pode dividirse por tres, cuxa suma de cifras é 1 + 2 = 3 e pode dividirse por tres. Outro exemplo é 273 xa que 2 + 7 + 3 = 12. Con todo, pretendemos concluír que todos os números cumpren esta propiedade. Por tanto, non basta con comprobar que é certo paira estes dous exemplos, e hai que atopar un razoamento baseado nas matemáticas. Se se consegue, demostrarase que o problema é certo paira calquera número (e ninguén poderá dicir que sexa falso).
O último teorema de Ferma propúxose cara a 1640. É un problema moi sinxelo de explicar, escrito por Fermat na esquina dun libro.
''Sexa n > 2 un número natural. Non existen números naturais a, b e c que cumpran a seguinte igualdade: an + bn = cn .''
Moitos matemáticos tentaron demostrar este problema, pero non o conseguiron ata que pasaron máis de 300 anos. O matemático Andrew Wiles demostrou en 1994 o último teorema de Fermat, e afirman que paira iso pasou oito anos traballando.
O último teorema de Fermat converteuse nun problema matemático famoso, xa que se fala non só do mundo das matemáticas, senón tamén de libros, películas, etc. Pero ademais do último teorema de Ferma, hai outros moitos problemas que son fáciles de explicar pero difíciles de resolver. Os problemas máis coñecidos son:
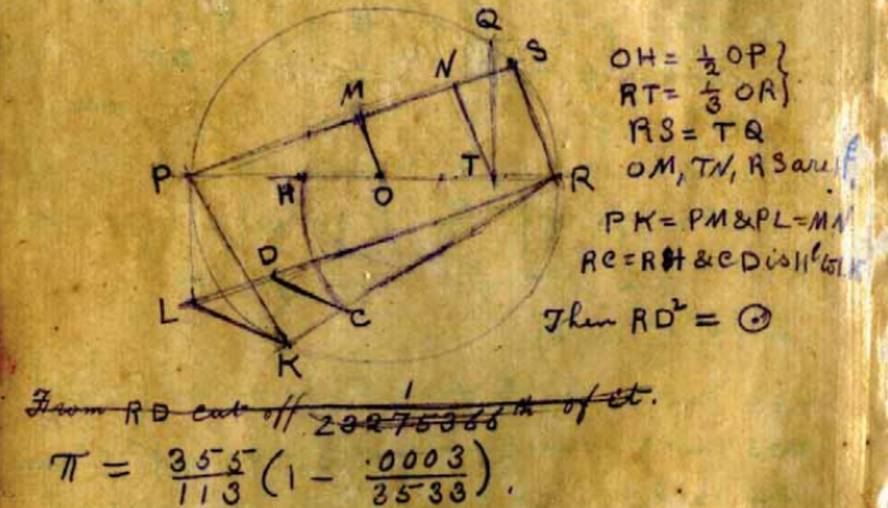
1. Cuadratura do círculo
O problema de cuadratura do círculo pódese presentar:
''Sexa o círculo de radio R. Utilizando só una regra e un compás debuxa un cadrado da mesma superficie do círculo.''
Os babilonios xa tiñan una aproximación a este problema. Xa no ano 500. Pero a resolución do problema foi presentada moito máis tarde por Ferdinand von Lindemann en 1882. Este matemático demostrou que o número tup é transcendente e con este resultado pódese concluír que o problema da cuadratura do círculo non é posible.
2. O problema das primeiras xemelgas numéricas
Os primeiros números só se poden dividir por un (1) e uno mesmo. Por exemplo, 7 números son o primeiro. Os primeiros números son ilimitados, é dicir, infinitos números son os primeiros. Este resultado foi probado por Euclides, a. C. No ano 300 escribiu no libro Elementos.
Dicimos que dous números a e b son os dous primeiros xemelgos se a distancia entre eles é dúas, é dicir, a = b + 2 ou b = a + 2. Por exemplo, 5 e 7 son os primeiros xemelgos. 11 e 13 tamén. O problema dos primeiros números xemelgos di:
''O número de números primarios xemelgos é infinito.''
Na actualidade este é un problema matemático aberto, é dicir, os matemáticos non conseguiron demostrar. E os primeiros números xemelgos máis grandes que se atoparon son 3756801695685 · 2666669 ± 1. Por tanto, considérase que os primeiros números xemelgos son ilimitados e ata que alguén demostre que é verdade ou falso seguirá sendo conjetivo.
3. Conxectura de Catalan
En primeiro lugar, quede claro que este problema non ten nada que ver cos habitantes de Cataluña. O problema exposto pola matemática Eugène Charles Catalan en 1884 di:
''Só hai una parella consecutiva e que é a recomposición dos números naturais: 23 e 32.'
As palabras e consecutivas dos números naturais 23 e 32 son oito e nove respectivamente. Ademais, a conxectura indica que non hai ningún número normal x, e, p e q que cumpra a igualdade xp – yq = 1. A pesar da fácil explicación deste problema, foi moi difícil demostralo paira os matemáticos, e finalmente foi o matemático Preda Mih??ilescu quen o demostrou en 2002.
4º Conxectura de Goldbach
O aiero de Goldbach di:
''Calquera número par maior que dous é a suma de dous números primos.''
Un exemplo: 10 = 3 + 7, onde 3 e 7 son os primeiros números. Outros exemplos coñecidos son 20 = 13 + 7 e 30 = 13 + 17. Habemos visto que estes números cumpren esta propiedade. Pero paira calquera número par dicir que iso é certo, fai falta una demostración.
Este problema apareceu por primeira vez nunha carta dirixida por Goldbach a Euler en 1742. Desde entón moitos matemáticos traballaron neste problema. Nos últimos anos, desenvolvéronse métodos numéricos moi complexos paira analizar o problema, e segundo estas análises, todos os números menores de 1018 cumpren o espírito de Goldbach. Por iso, a maioría dos matemáticos cre que esta solución é certa, pero aínda non atoparon probas.
Vimos problemas fáciles de explicar pero moi difíciles de resolver, e aínda que existen moitos destes problemas, neste artigo pensei escribir só algúns exemplos. Doutra banda, coñezo problemas matemáticos difíciles de explicar e fáciles de resolver, pero que coa vosa autorización verémolos noutro momento.
Referencias
''Os primeiros xemelgos''. Revista Elhuyar. 01/08/2008. 'Sobre o último teorema de Fermat.'' Revista Elhuyar. 01/05/1995 Autor: Javier Duoandikoetxea Zuazo. 'John Harper, investigando matemáticas e patos'. Lingua Castelá. 15/11/2015 Autor: Josu Doncel Vicente. 'Modular elliptic curves and Fermat's Last Theorem'.Annals of Mathematics 142 (2). Autor: Andrew Willes. 'Uever die Zahl pi'. 20 (2) de Mathematische Annal. Autor: Ferdinand von Lindemann.



_display_home.JPG)





