Problemas matemáticos fáciles de entender pero difíciles de resolver
Los matemáticos investigan problemas de ingeniería, biología, etc. Y es que gracias a demostraciones basadas en las matemáticas, podemos entender el comportamiento de los fenómenos que se producen en el mundo y en la naturaleza.
A veces, los problemas que se estudian en matemáticas están compuestos por ecuaciones gigantes, por lo que mucha gente cree que son muy difíciles de resolver. Otros problemas son muy fáciles de entender (en muchos casos pueden aparecer en una línea), pero los matemáticos han pasado años buscando su demostración. Por tanto, podemos decir que son muy difíciles de resolver. En este artículo hablaremos sobre problemas matemáticos fácilmente explicables (e incluso comprensibles) pero difíciles de demostrar.
Dejad que explique qué es resolver un problema matemático. Supongamos que queremos resolver el problema denominado X. ¿Cómo se hace? Para demostrar que X es falsa basta con encontrar un ejemplo. Por ejemplo, consideremos el problema: ''todos los números son normales''. Para demostrar que esto es falso hay que dar un número que no sea normal, por ejemplo 3/2. Con ello podemos concluir que no todos los números son normales. Pero para concluir que X es cierto necesitamos una demostración. Consideremos el problema: ''la suma de las cifras de todos los números divisibles por tres se puede dividir por tres''. Por ejemplo, el número 12 puede dividirse por tres, cuya suma de cifras es 1 + 2 = 3 y puede dividirse por tres. Otro ejemplo es 273 ya que 2 + 7 + 3 = 12. Sin embargo, pretendemos concluir que todos los números cumplen esta propiedad. Por lo tanto, no basta con comprobar que es cierto para estos dos ejemplos, y hay que encontrar un razonamiento basado en las matemáticas. Si se consigue, se demostrará que el problema es cierto para cualquier número (y nadie podrá decir que sea falso).
El último teorema de Ferma se propuso hacia 1640. Es un problema muy sencillo de explicar, escrito por Fermat en la esquina de un libro.
''Sea n > 2 un número natural. No existen números naturales a, b y c que cumplan la siguiente igualdad: an + bn = cn .''
Muchos matemáticos intentaron demostrar este problema, pero no lo consiguieron hasta que pasaron más de 300 años. El matemático Andrew Wiles demostró en 1994 el último teorema de Fermat, y afirman que para ello pasó ocho años trabajando.
El último teorema de Fermat se ha convertido en un problema matemático famoso, ya que se habla no sólo del mundo de las matemáticas, sino también de libros, películas, etc. Pero además del último teorema de Ferma, hay otros muchos problemas que son fáciles de explicar pero difíciles de resolver. Los problemas más conocidos son:
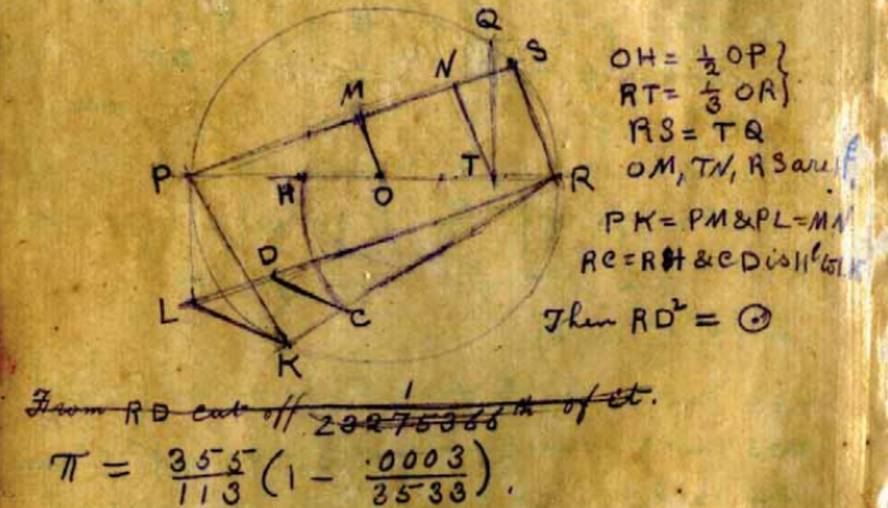
1. Cuadratura del círculo
El problema de cuadratura del círculo se puede presentar:
''Sea el círculo de radio R. Utilizando sólo una regla y un compás dibuja un cuadrado de la misma superficie del círculo.''
Los babilonios ya tenían una aproximación a este problema. Ya en el año 500. Pero la resolución del problema fue presentada mucho más tarde por Ferdinand von Lindemann en 1882. Este matemático demostró que el número tup es trascendente y con este resultado se puede concluir que el problema de la cuadratura del círculo no es posible.
2. El problema de las primeras gemelas numéricas
Los primeros números sólo se pueden dividir por uno (1) y uno mismo. Por ejemplo, 7 números son el primero. Los primeros números son ilimitados, es decir, infinitos números son los primeros. Este resultado fue probado por Euclides, a. C. En el año 300 escribió en el libro Elementos.
Decimos que dos números a y b son los dos primeros gemelos si la distancia entre ellos es dos, es decir, a = b + 2 o b = a + 2. Por ejemplo, 5 y 7 son los primeros gemelos. 11 y 13 también. El problema de los primeros números gemelos dice:
''El número de números primarios gemelos es infinito.''
En la actualidad este es un problema matemático abierto, es decir, los matemáticos no han conseguido demostrar. Y los primeros números gemelos más grandes que se han encontrado son 3756801695685 · 2666669 ± 1. Por lo tanto, se considera que los primeros números gemelos son ilimitados y hasta que alguien demuestre que es verdad o falso seguirá siendo conjetivo.
3. Conjetura de Catalan
En primer lugar, quede claro que este problema no tiene nada que ver con los habitantes de Cataluña. El problema planteado por la matemática Eugène Charles Catalan en 1884 dice:
''Sólo hay una pareja consecutiva y que es la recomposición de los números naturales: 23 y 32.'
Las palabras y consecutivas de los números naturales 23 y 32 son ocho y nueve respectivamente. Además, la conjetura indica que no hay ningún número normal x, y, p y q que cumpla la igualdad xp – yq = 1. A pesar de la fácil explicación de este problema, fue muy difícil demostrarlo para los matemáticos, y finalmente fue el matemático Preda Mih??ilescu quien lo demostró en 2002.
4º Conjetura de Goldbach
El aiero de Goldbach dice:
''Cualquier número par mayor que dos es la suma de dos números primos.''
Un ejemplo: 10 = 3 + 7, donde 3 y 7 son los primeros números. Otros ejemplos conocidos son 20 = 13 + 7 y 30 = 13 + 17. Hemos visto que estos números cumplen esta propiedad. Pero para cualquier número par decir que eso es cierto, hace falta una demostración.
Este problema apareció por primera vez en una carta dirigida por Goldbach a Euler en 1742. Desde entonces muchos matemáticos han trabajado en este problema. En los últimos años, se han desarrollado métodos numéricos muy complejos para analizar el problema, y según estos análisis, todos los números menores de 1018 cumplen el espíritu de Goldbach. Por ello, la mayoría de los matemáticos cree que esta solución es cierta, pero todavía no han encontrado pruebas.
Hemos visto problemas fáciles de explicar pero muy difíciles de resolver, y aunque existen muchos de estos problemas, en este artículo he pensado escribir sólo algunos ejemplos. Por otro lado, conozco problemas matemáticos difíciles de explicar y fáciles de resolver, pero que con vuestra autorización los veremos en otro momento.
Referencias
''Los primeros gemelos''. Revista Elhuyar. 01/08/2008. 'Sobre el último teorema de Fermat.'' Revista Elhuyar. 01/05/1995 Autor: Javier Duoandikoetxea Zuazo. 'John Harper, investigando matemáticas y patos'. Lengua Castellana. 15/11/2015 Autor: Josu Doncel Vicente. 'Modular elliptic curves and Fermat's Last Theorem'.Annals of Mathematics 142 (2). Autor: Andrew Willes. 'Uever die Zahl pi'. 20 (2) de Mathematische Annal. Autor: Ferdinand von Lindemann.



_display_home.JPG)





