O mellor teorema de Noether
Os matemáticos coñecen máis dun teorema de Noether. De feito, o apelido Noether é portado por unha famosa familia de matemáticos. Pero entre todos existe un teorema de Noether especialmente bonito. Emmy é de Noether.
Amalie Emmy Noether naceu en Alemaña en 1882. Paira moitos é a muller matemática máis grande da historia. A pesar das dificultades, conseguiu aprender matemáticas (xa que estaba prohibido paira as mulleres da época); ao estar tamén prohibido ser profesor, deu clases en substitución do seu amigo David Hilbert. En palabras de Einstein, Noether é o maior xenio das matemáticas desde que comezou o ensino superior feminina. En 1918, Noether publicou o seu teorema máis famoso. Paira moitos expertos, o teorema máis belo e profundo que ten a física matemática.
É belo porque nos mostra a base dos principios de conservación que se coñecían desde hai tempo, facendo ver que moitos principios diferentes teñen a mesma base. E profunda, porque combina dúas ideas que en principio parecen moi diferentes: os principios de simetría e conservación.
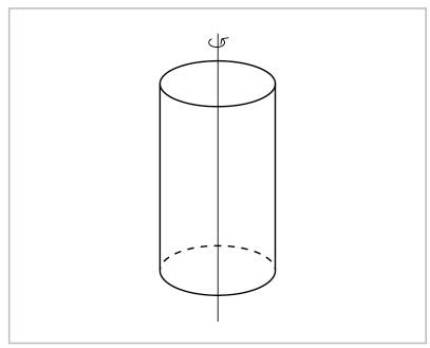
A idea de simetría é moi básica: una cousa de simetría vémola igual antes e despois do exercicio de simetría. Un cilindro, por exemplo, verémolo igual se se produce calquera rotación sobre o seu eixo. Non podemos distinguir entre o cilindro anterior e o posterior á rotación.
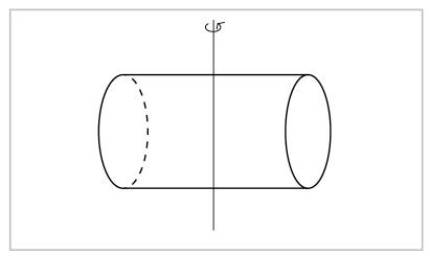
Se viramos ao redor doutro eixo, pola contra, non veremos o cilindro igual. Podemos saber se alguén virou ou non.
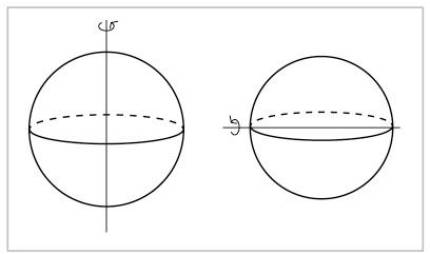
Una esfera é un obxecto aínda máis simétrico. Virando ao redor de calquera eixo que pase polo seu centro, verémolo igual.
Hai que mencionar dous tipos de simetría: as simetrías continuas e as simetrías discretas. En matemáticas, seguir significa que dous obxectos do que se seguiu poden estar tan cerca como se queira. Por tanto, nunha simetría continua, dúas operacións de simetría están moi próximas entre si. Nos casos dos eixos da esfera e do cilindro, todas as rotacións son de simetría, aínda que sexan mínimas. E hai una operación de simetría moi próxima a unha operación de simetría. Na segunda figura, para que una rotación sexa simétrica debe ser de 180 graos, polo que moi preto dunha rotación de simetría non hai outra rotación de simetría. Esta simetría é discreta.
Un principio de conservación dinos que o valor dunha magnitude física non varía. Todos ouvimos falar do principio de conservación da enerxía: a enerxía non se pode producir nin destruír. Nun sistema físico, a enerxía (si está illada) non cambia co tempo. Tamén se coñecían outros moitos principios de conservación. a principios do século XX: principio de conservación do momento lineal e principio de conservación do momento angular, por citar os máis importantes.
Os físicos buscan este tipo de principios porque lles axudan a comprender mellor os seus sistemas. Por exemplo, grazas ao principio de conservación da enerxía, somos capaces de explicar por que os planetas van máis rápido no seu elipse ao redor do sol, cando están máis cerca do sol que cando están máis lonxe (este principio dá una explicación á famosa lei de Kepler). E aínda por riba, somos capaces de adiviñar a velocidade dos planetas nun punto e outro. Algo parecido ocorre cos átomos: somos capaces de saber a cor de luz que emitirá un átomo dunha determinada especie química, atendendo simplemente ao principio de conservación da enerxía.
O principio de conservación do momento lineal permítenos coñecer a velocidade coa que sairán os obxectos chocados tras un choque. Isto pode servir, por exemplo, paira coñecer a velocidade dos vehículos nun accidente de tráfico ou paira controlar os detalles da colisión que creou o bosón de Higgs.
A conservación do momento angular ten, entre outros moitos, una bonita consecuencia: a órbita dun planeta ao redor do sol atópase nun plano. É dicir, un planeta nunca pode saír dese plano. O plano da órbita da Terra chámase eclíptica. Esta palabra será coñecida polos afeccionados á astronomía, xa que é tamén o nome da traxectoria do sol no ceo e as constelacións do zodiaco están situadas nel. Pois se non fóra polo principio de conservación do momento angular, a órbita da Terra non estaría na Eclíptica e desprazaríase por encima e por baixo dese plano saíndo do plano.
XX. A principios do século XX coñecíanse algúns destes principios de conservación. Naquela época, Noether deu a estes principios un significado sorprendente. Enunciaremos una versión informal da súa teorema:
“Calquera simetría continua dun sistema responde a un principio de conservación”.
Noether achegou a demostración do teorema (neste artigo non o imos a dar porque é moi técnico). Paira comprender mellor o significado e a profundidade desta frase, poñamos como exemplo as simetrías máis importantes da física: as simetrías do tempo espacial.
Antes de empezar, que é una simetría do tempo espacial? Pois imaxinemos un espazo baleiro. O espazo interestelar, se queremos, onde non hai gravidade. Que cambios xeométricos podemos facer a este espazo? Pois por exemplo, podemos facer una translación espacial. É dicir, podemos movernos en calquera dirección a certa distancia. En física hai un principio, chamado principio da relatividad, que nos di que todas as leis da física teñen que ser iguais nesta nova posición. Se non fosen iguais, o resultado dun experimento sería diferente nunha ou outra posición. Por exemplo, os electróns dun átomo situaríanse de forma diferente na nosa habitación, na casa do noso veciño ou na galaxia de Andrómeda. Nunca o vimos así, polo que pensamos que as leis da física son as mesmas en todos os puntos do espazo e, por tanto, os resultados de todos os experimentos son os mesmos en calquera lugar. Por iso dicimos que é una simetría do espazo, porque un punto do espazo non se pode separar de todos os demais.
O principio da relatividad dános conta doutras simetrías: nunca ninguén viu una lei da física que cambia co tempo. Leis da electricidade, por exemplo, o XIX. Establecéronse no século XIX e hoxe en día seguen sendo idénticas (chamadas leis de Maxwell). Non se modificaron. É máis, temos poderosas razóns paira pensar que no pasado tamén existiron varios millóns de anos de leis. Este fenómeno denomínase simetría coas translacións temporais. Una translación temporal paira o pasado ou paira o futuro non pode cambiar a lei da física. O resultado dun experimento será hoxe, onte ou mañá.
Temos pois dous simetrías que nos deu o principio da relatividad: as translacións espaciais e as translacións temporais. Existe una terceira simetría que nos dá o principio de relatividad: a simetría coas rotacións. Todas as leis da física son iguais se tomásemos todo o sistema e facémolo virar. É dicir, o espazo non ten una dirección privilexiada, á que se mira una física diferente que calquera outra dirección.
Por tanto, segundo o principio de relatividad, o espazo non ten lugar privilexiado, non ten momento privilexiado e non ten dirección privilexiada. O resultado de todo experimento, como o choque entre dous electróns ou o estado de tres quarks que forman un protón, é idéntico en todos os puntos do espazo, en todos os momentos do tempo e en todas as direccións do espazo. Se pechásemos os ollos e fixésemos una rotación, una translación temporal ou una translación espacial, en ningún caso sería posible saber se se produciu esta operación ao reabrirse. Estas son as simetrías do tempo espacial que establece o principio da relatividad (xa que o principio da relatividad dános conta de máis simetrías, pero non as mencionaremos neste artigo paira non confundir demasiado).
Estas tres simetrías son continuas. No caso das translacións espaciais, podemos facer una translación moi pequena e quedarnos nun punto moi próximo. No caso das translacións de tempo tamén podemos “movernos” a un momento moi próximo (non hai saltos descontinuos no espazo e no tempo). E elixindo un eixo, podemos realizar una pequena rotación ao redor do mesmo. Por tanto, ao tratarse de simetrías continuas, pódese aplicar o teorema de Noether.
E cales serían as magnitudes conservadas correspondentes a estas simetrías? Pois ben, o propio teorema dinos que no caso das translacións espaciais, a magnitude que se conserva é o momento lineal. No caso das translacións de tempo, enerxía. E no caso das rotacións, o momento angular. Que bo resultado!
Noether descubriu una relación profunda e sorprendente entre as simetrías e os principios de conservación: son consecuencia da outra! Ambos van xuntos, non se poden separar. Nun mundo onde a enerxía non se conservaría, as leis da física desenvolveríanse co tempo, é dicir, iríanse modificando no tempo. Dous momentos diferentes do tempo non serían inseparables.
Aínda que non os mencionamos neste artigo, xa que falamos unicamente das simetrías do tempo espacial, este teorema é aplicable a todas as demais simetrías. Paira espertar a curiosidade do público lector diremos que a conservación da carga eléctrica tamén é consecuencia do teorema de Noether. Neste caso, a simetría non é o tempo espacial, senón o propio sistema de ecuacións, e a esta simetría máis abstracta chámaselle simetría gauge. Isto pode incluír una interpretación xeométrica nun espazo de máis de catro dimensións. Pero iso é cuestión de deixalo paira outro día.
Como dixo Robert Wald, una vez que se deu conta diso, non pode evitar que un poida sentir que aprendeu algo moi profundo sobre como actúa a natureza. Ese é, por tanto, o agasallo que nos deixou esta gran muller.