Le meilleur théorème de Noether
Les mathématiciens connaissent plus d'un théorème de Noether. En fait, le nom de famille Noether est porté par une célèbre famille de mathématiciens. Mais parmi tous il y a un théorème de Noether particulièrement beau. Emmy est de Noether.
Amalie Emmy Noether est née en Allemagne en 1882. Pour beaucoup, il est la plus grande femme mathématique de l'histoire. Malgré les difficultés, il a réussi à apprendre les mathématiques (car il était interdit pour les femmes de l'époque); étant également interdit d'être professeur, il a enseigné en remplacement de son ami David Hilbert. Selon les mots d'Einstein, Noether est le plus grand génie des mathématiques depuis qu'il a commencé l'enseignement supérieur féminin. En 1918, Noether a publié son théorème le plus célèbre. Pour de nombreux experts, le plus beau et le plus profond théorème a la physique mathématique.
C'est beau parce qu'il nous montre la base des principes de conservation qui étaient connus depuis longtemps, faisant voir que beaucoup de principes différents ont la même base. Et profond, parce qu'il combine deux idées qui en principe semblent très différentes: les principes de symétrie et de conservation.
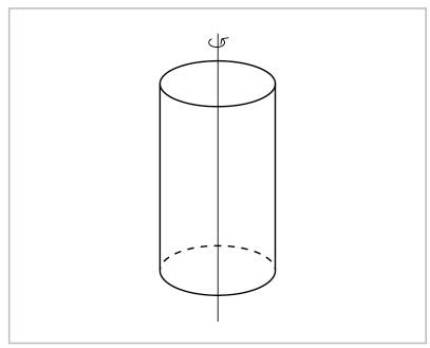
L'idée de symétrie est très basique: une chose de symétrie nous la voyons égale avant et après l'exercice de symétrie. Un cylindre, par exemple, nous verrons la même chose si une rotation se produit sur son axe. Nous ne pouvons pas distinguer entre le cylindre précédent et le cylindre postérieur à la rotation.
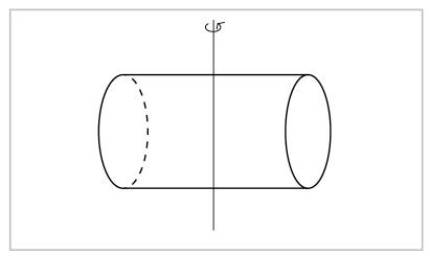
Si nous tournons autour d'un autre axe, nous ne verrons pas le cylindre égal. Nous pouvons savoir si quelqu'un a tourné ou non.
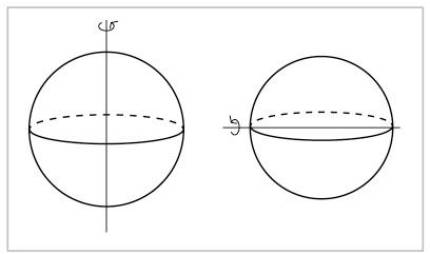
Une sphère est un objet encore plus symétrique. En tournant autour de n'importe quel axe qui passe par son centre, nous verrons la même chose.
Il faut mentionner deux types de symétrie : les symétries continues et les symétries discrètes. En mathématiques, suivre signifie que deux objets dont vous avez suivi peuvent être aussi proches que vous le souhaitez. Par conséquent, dans une symétrie continue, deux opérations de symétrie sont très proches les unes des autres. Dans les cas des axes de la sphère et du cylindre, toutes les rotations sont symétriques, même minimes. Et il y a une opération de symétrie très proche d'une opération de symétrie. Dans la deuxième figure, pour qu'une rotation soit symétrique doit être de 180 degrés, donc très proche d'une rotation de symétrie il n'y a pas d'autre rotation de symétrie. Cette symétrie est discrète.
Un principe de conservation nous dit que la valeur d'une grandeur physique ne varie pas. Nous avons tous entendu parler du principe de conservation de l'énergie : l'énergie ne peut être produite ni détruite. Dans un système physique, l'énergie (si elle est isolée) ne change pas avec le temps. De nombreux autres principes de conservation étaient également connus. au début du XXe siècle: principe de conservation du moment linéaire et principe de conservation du moment angulaire, pour citer les plus importants.
Les physiciens recherchent ce type de principes car ils les aident à mieux comprendre leurs systèmes. Par exemple, grâce au principe de conservation de l'énergie, nous sommes en mesure d'expliquer pourquoi les planètes vont plus vite dans leur ellipse autour du soleil, quand elles sont plus proches du soleil que lorsqu'elles sont plus loin (ce principe explique la célèbre loi de Kepler). Et si c'était peu, nous sommes capables de deviner la vitesse des planètes à un point et un autre. Quelque chose de semblable se produit avec les atomes: nous sommes capables de connaître la couleur de lumière qui émettra un atome d'une espèce chimique donnée, en tenant simplement au principe de conservation de l'énergie.
Le principe de conservation du moment linéaire nous permet de connaître la vitesse avec laquelle les objets collisés sortiront après un choc. Cela peut servir, par exemple, à connaître la vitesse des véhicules dans un accident de voiture ou à contrôler les détails de la collision qui a créé le boson de Higgs.
La conservation du moment angulaire a, entre autres, une belle conséquence : l'orbite d'une planète autour du soleil se trouve sur un plan. Autrement dit, une planète ne peut jamais quitter ce plan. Le plan de l'orbite terrestre est appelé écliptique. Ce mot sera connu par les amateurs d'astronomie, car il est aussi le nom de la trajectoire du soleil dans le ciel et les constellations du zodiaque sont situés en elle. Si ce n'était pas par le principe de conservation du moment angulaire, l'orbite de la Terre ne serait pas dans l'Écliptique et se déplacerait au-dessus et au-dessous de ce plan en sortant du plan.
XX. Au début du XXe siècle, certains de ces principes de conservation étaient connus. À cette époque, Noether donna à ces principes une signification étonnante. Nous énoncerons une version informelle de son théorème:
“Toute symétrie continue d’un système répond à un principe de conservation”.
Noether a apporté la démonstration du théorème (dans cet article, nous ne le donnerons pas parce qu'il est très technique). Pour mieux comprendre la signification et la profondeur de cette phrase, prenons comme exemple les symétries les plus importantes de la physique : les symétries du temps spatial.
Avant de commencer, qu'est-ce qu'une symétrie du temps spatial ? Imaginons donc un espace vide. L'espace interstellaire, si nous le voulons, où il n'y a pas de gravité. Quels changements géométriques pouvons-nous faire à cet espace ? Par exemple, nous pouvons effectuer une translation spatiale. Autrement dit, nous pouvons nous déplacer dans n'importe quelle direction à une certaine distance. En physique, il y a un principe, appelé principe de la relativité, qui nous dit que toutes les lois de la physique doivent être égales dans cette nouvelle position. S'ils n'étaient pas égaux, le résultat d'une expérience serait différent dans une position ou une autre. Par exemple, les électrons d'un atome se situeraient différemment dans notre chambre, dans la maison de notre voisin ou dans la galaxie d'Andromède. Nous ne l'avons jamais vu ainsi, donc nous pensons que les lois de la physique sont les mêmes à tous les points de l'espace et donc les résultats de toutes les expériences sont les mêmes partout. C'est pourquoi nous disons que c'est une symétrie de l'espace, car un point de l'espace ne peut être séparé de tous les autres.
Le principe de la relativité nous rend compte d'autres symétries: personne n'a jamais vu une loi de la physique qui change avec le temps. Lois de l'électricité, par exemple, le XIX. Ils ont été établis au XIXe siècle et sont encore aujourd'hui identiques (soi-disant lois de Maxwell). Ils n'ont pas été modifiés. De plus, nous avons de puissantes raisons de penser que plusieurs millions d'années de lois ont également existé dans le passé. Ce phénomène est appelé symétrie avec les translations temporaires. Une translation temporaire pour le passé ou pour le futur ne peut pas changer la loi de la physique. Le résultat d'une expérience sera aujourd'hui, hier ou demain.
Nous avons donc deux symétries qui nous ont donné le principe de la relativité: les translations spatiales et les translations temporelles. Il y a une troisième symétrie qui nous donne le principe de la relativité: la symétrie avec les rotations. Toutes les lois de la physique sont égales si nous prenons tout le système et le faisons tourner. C'est-à-dire que l'espace n'a pas une direction privilégiée, à laquelle on regarde une physique différente que n'importe quelle autre direction.
Donc, selon le principe de relativité, l'espace n'a pas de place privilégiée, il n'a pas de moment privilégié et il n'a pas de direction privilégiée. Le résultat de toute expérience, comme le choc entre deux électrons ou l'état de trois quarks formant un proton, est identique à tous les points de l'espace, à tous les moments du temps et dans toutes les directions de l'espace. Si nous fermons les yeux et faisons une rotation, une translation temporaire ou une translation spatiale, il ne serait en aucun cas possible de savoir si cette opération a eu lieu lors de la réouverture. Ce sont les symétries du temps spatial qui établit le principe de la relativité (puisque le principe de la relativité nous rend compte de plus de symétries, mais nous ne les mentionnerons pas dans cet article pour ne pas trop confondre).
Ces trois symétries sont continues. Dans le cas des translations spatiales, nous pouvons faire une traduction très petite et rester à un point très proche. Dans le cas des translations de temps, nous pouvons aussi “bouger” à un moment très proche (il n’y a pas de sauts discontinus dans l’espace et dans le temps). Et en choisissant un axe, nous pouvons faire une petite rotation autour de celui-ci. Par conséquent, comme il s'agit de symétries continues, on peut appliquer le théorème de Noether.
Et quelles seraient les grandeurs conservées correspondant à ces symétries ? Eh bien, le théorème lui-même nous dit que dans le cas des translations spatiales, l'ampleur qui est conservé est le moment linéaire. Dans le cas des translations de temps, énergie. Et dans le cas des rotations, le moment angulaire. Quel bon résultat !
Noether a découvert une relation profonde et surprenante entre les symétries et les principes de conservation: Ils sont la conséquence de l'autre! Les deux vont ensemble, ils ne peuvent pas être séparés. Dans un monde où l'énergie ne serait pas conservée, les lois de la physique se développeraient au fil du temps, c'est-à-dire qu'elles seraient modifiées dans le temps. Deux moments différents du temps ne seraient pas inséparables.
Bien que nous ne les avons pas mentionnés dans cet article, puisque nous avons parlé uniquement des symétries du temps spatial, ce théorème est applicable à toutes les autres symétries. Pour éveiller la curiosité du public lecteur, nous dirons que la conservation de la charge électrique est également une conséquence du théorème de Noether. Dans ce cas, la symétrie n'est pas le temps spatial, mais le système d'équations lui-même, et cette symétrie plus abstraite est appelée symétrie gauge. Cela peut inclure une interprétation géométrique dans un espace de plus de quatre dimensions. Mais c'est une question de le laisser pour un autre jour.
Comme l'a dit Robert Wald, une fois qu'il s'en est rendu compte, il ne peut empêcher que l'on puisse sentir qu'il a appris quelque chose de très profond sur la façon dont la nature agit. C'est donc le cadeau que nous a laissé cette grande femme.