El mejor teorema de Noether
Los matemáticos conocen más de un teorema de Noether. De hecho, el apellido Noether es portado por una famosa familia de matemáticos. Pero entre todos existe un teorema de Noether especialmente bonito. Emmy es de Noether.
Amalie Emmy Noether nació en Alemania en 1882. Para muchos es la mujer matemática más grande de la historia. A pesar de las dificultades, consiguió aprender matemáticas (ya que estaba prohibido para las mujeres de la época); al estar también prohibido ser profesor, dio clases en sustitución de su amigo David Hilbert. En palabras de Einstein, Noether es el mayor genio de las matemáticas desde que comenzó la enseñanza superior femenina. En 1918, Noether publicó su teorema más famoso. Para muchos expertos, el teorema más bello y profundo que tiene la física matemática.
Es bello porque nos muestra la base de los principios de conservación que se conocían desde hace tiempo, haciendo ver que muchos principios diferentes tienen la misma base. Y profunda, porque combina dos ideas que en principio parecen muy diferentes: los principios de simetría y conservación.
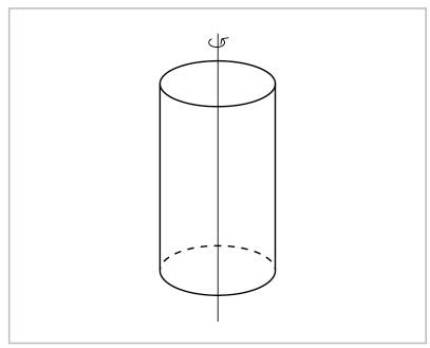
La idea de simetría es muy básica: una cosa de simetría la vemos igual antes y después del ejercicio de simetría. Un cilindro, por ejemplo, lo veremos igual si se produce cualquier rotación sobre su eje. No podemos distinguir entre el cilindro anterior y el posterior a la rotación.
Si giramos alrededor de otro eje, por el contrario, no veremos el cilindro igual. Podemos saber si alguien ha girado o no.
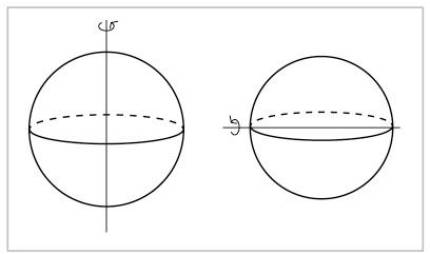
Una esfera es un objeto aún más simétrico. Girando alrededor de cualquier eje que pase por su centro, lo veremos igual.
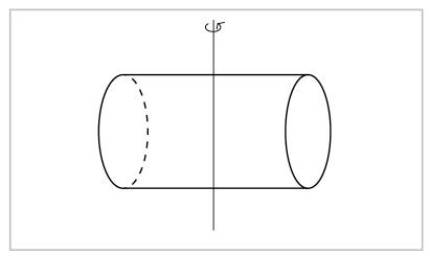
Hay que mencionar dos tipos de simetría: las simetrías continuas y las simetrías discretas. En matemáticas, seguir significa que dos objetos de lo que se ha seguido pueden estar tan cerca como se quiera. Por tanto, en una simetría continua, dos operaciones de simetría están muy próximas entre sí. En los casos de los ejes de la esfera y del cilindro, todas las rotaciones son de simetría, aunque sean mínimas. Y hay una operación de simetría muy próxima a una operación de simetría. En la segunda figura, para que una rotación sea simétrica debe ser de 180 grados, por lo que muy cerca de una rotación de simetría no hay otra rotación de simetría. Esta simetría es discreta.
Un principio de conservación nos dice que el valor de una magnitud física no varía. Todos hemos oído hablar del principio de conservación de la energía: la energía no se puede producir ni destruir. En un sistema físico, la energía (si está aislada) no cambia con el tiempo. También se conocían otros muchos principios de conservación. a principios del siglo XX: principio de conservación del momento lineal y principio de conservación del momento angular, por citar los más importantes.
Los físicos buscan este tipo de principios porque les ayudan a comprender mejor sus sistemas. Por ejemplo, gracias al principio de conservación de la energía, somos capaces de explicar por qué los planetas van más rápido en su elipse alrededor del sol, cuando están más cerca del sol que cuando están más lejos (este principio da una explicación a la famosa ley de Kepler). Y por si fuera poco, somos capaces de adivinar la velocidad de los planetas en un punto y otro. Algo parecido ocurre con los átomos: somos capaces de saber el color de luz que emitirá un átomo de una determinada especie química, atendiendo simplemente al principio de conservación de la energía.
El principio de conservación del momento lineal nos permite conocer la velocidad con la que saldrán los objetos colisionados tras un choque. Esto puede servir, por ejemplo, para conocer la velocidad de los vehículos en un accidente de tráfico o para controlar los detalles de la colisión que creó el bosón de Higgs.
La conservación del momento angular tiene, entre otros muchos, una bonita consecuencia: la órbita de un planeta alrededor del sol se encuentra en un plano. Es decir, un planeta nunca puede salir de ese plano. El plano de la órbita de la Tierra se llama eclíptica. Esta palabra será conocida por los aficionados a la astronomía, ya que es también el nombre de la trayectoria del sol en el cielo y las constelaciones del zodiaco están situadas en él. Pues si no fuera por el principio de conservación del momento angular, la órbita de la Tierra no estaría en la Eclíptica y se desplazaría por encima y por debajo de ese plano saliendo del plano.
XX. A principios del siglo XX se conocían algunos de estos principios de conservación. En aquella época, Noether dio a estos principios un significado sorprendente. Enunciaremos una versión informal de su teorema:
“Cualquier simetría continua de un sistema responde a un principio de conservación”.
Noether aportó la demostración del teorema (en este artículo no lo vamos a dar porque es muy técnico). Para comprender mejor el significado y la profundidad de esta frase, pongamos como ejemplo las simetrías más importantes de la física: las simetrías del tiempo espacial.
Antes de empezar, ¿qué es una simetría del tiempo espacial? Pues imaginemos un espacio vacío. El espacio interestelar, si queremos, donde no hay gravedad. ¿Qué cambios geométricos podemos hacer a este espacio? Pues por ejemplo, podemos hacer una traslación espacial. Es decir, podemos movernos en cualquier dirección a cierta distancia. En física hay un principio, llamado principio de la relatividad, que nos dice que todas las leyes de la física tienen que ser iguales en esta nueva posición. Si no fueran iguales, el resultado de un experimento sería diferente en una u otra posición. Por ejemplo, los electrones de un átomo se ubicarían de forma diferente en nuestra habitación, en la casa de nuestro vecino o en la galaxia de Andrómeda. Nunca lo hemos visto así, por lo que pensamos que las leyes de la física son las mismas en todos los puntos del espacio y, por tanto, los resultados de todos los experimentos son los mismos en cualquier lugar. Por eso decimos que es una simetría del espacio, porque un punto del espacio no se puede separar de todos los demás.
El principio de la relatividad nos da cuenta de otras simetrías: nunca nadie ha visto una ley de la física que cambia con el tiempo. Leyes de la electricidad, por ejemplo, el XIX. Se establecieron en el siglo XIX y hoy en día siguen siendo idénticas (llamadas leyes de Maxwell). No se han modificado. Es más, tenemos poderosas razones para pensar que en el pasado también han existido varios millones de años de leyes. Este fenómeno se denomina simetría con las traslaciones temporales. Una traslación temporal para el pasado o para el futuro no puede cambiar la ley de la física. El resultado de un experimento será hoy, ayer o mañana.
Tenemos pues dos simetrías que nos ha dado el principio de la relatividad: las traslaciones espaciales y las traslaciones temporales. Existe una tercera simetría que nos da el principio de relatividad: la simetría con las rotaciones. Todas las leyes de la física son iguales si tomáramos todo el sistema y lo hacemos girar. Es decir, el espacio no tiene una dirección privilegiada, a la que se mira una física diferente que cualquier otra dirección.
Por tanto, según el principio de relatividad, el espacio no tiene lugar privilegiado, no tiene momento privilegiado y no tiene dirección privilegiada. El resultado de todo experimento, como el choque entre dos electrones o el estado de tres quarks que forman un protón, es idéntico en todos los puntos del espacio, en todos los momentos del tiempo y en todas las direcciones del espacio. Si cerráramos los ojos y hiciéramos una rotación, una traslación temporal o una traslación espacial, en ningún caso sería posible saber si se ha producido esta operación al reabrirse. Estas son las simetrías del tiempo espacial que establece el principio de la relatividad (ya que el principio de la relatividad nos da cuenta de más simetrías, pero no las mencionaremos en este artículo para no confundir demasiado).
Estas tres simetrías son continuas. En el caso de las traslaciones espaciales, podemos hacer una traslación muy pequeña y quedarnos en un punto muy cercano. En el caso de las traslaciones de tiempo también podemos “movernos” a un momento muy cercano (no hay saltos discontinuos en el espacio y en el tiempo). Y eligiendo un eje, podemos realizar una pequeña rotación alrededor del mismo. Por tanto, al tratarse de simetrías continuas, se puede aplicar el teorema de Noether.
¿Y cuáles serían las magnitudes conservadas correspondientes a estas simetrías? Pues bien, el propio teorema nos dice que en el caso de las traslaciones espaciales, la magnitud que se conserva es el momento lineal. En el caso de las traslaciones de tiempo, energía. Y en el caso de las rotaciones, el momento angular. ¡Qué buen resultado!
Noether descubrió una relación profunda y sorprendente entre las simetrías y los principios de conservación: ¡son consecuencia de la otra! Ambos van juntos, no se pueden separar. En un mundo donde la energía no se conservaría, las leyes de la física se desarrollarían con el tiempo, es decir, se irían modificando en el tiempo. Dos momentos diferentes del tiempo no serían inseparables.
Aunque no los hemos mencionado en este artículo, ya que hemos hablado únicamente de las simetrías del tiempo espacial, este teorema es aplicable a todas las demás simetrías. Para despertar la curiosidad del público lector diremos que la conservación de la carga eléctrica también es consecuencia del teorema de Noether. En este caso, la simetría no es el tiempo espacial, sino el propio sistema de ecuaciones, y a esta simetría más abstracta se le llama simetría gauge. Esto puede incluir una interpretación geométrica en un espacio de más de cuatro dimensiones. Pero eso es cuestión de dejarlo para otro día.
Como dijo Robert Wald, una vez que se ha dado cuenta de ello, no puede evitar que uno pueda sentir que ha aprendido algo muy profundo sobre cómo actúa la naturaleza. Ese es, por tanto, el regalo que nos dejó esta gran mujer.