Noether's best theorem
Mathematicians know more than one Noether theorem. In fact, the surname Noether is worn by a famous family of mathematicians. But among all there is a particularly beautiful Noether theorem. Emmy is from Noether.
Amalie Emmy Noether was born in Germany in 1882. For many it is the largest mathematical woman in history. Despite the difficulties, he managed to learn mathematics (since it was forbidden for the women of the time); being also forbidden to be a teacher, he taught instead of his friend David Hilbert. In Einstein's words, Noether is the greatest genius of mathematics since he began female higher education. In 1918, Noether published his most famous theorem. For many experts, the most beautiful and profound theorem that mathematical physics has.
It is beautiful because it shows us the basis of conservation principles that have long been known, showing that many different principles have the same basis. And deep, because it combines two ideas that in principle seem very different: the principles of symmetry and conservation.
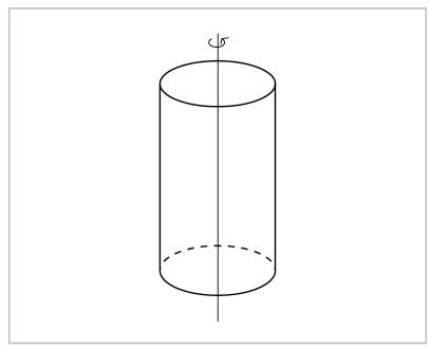
The idea of symmetry is very basic: one thing of symmetry is the same before and after the exercise of symmetry. A cylinder, for example, will look the same if any rotation occurs on its axis. We cannot distinguish between the cylinder before and after rotation.
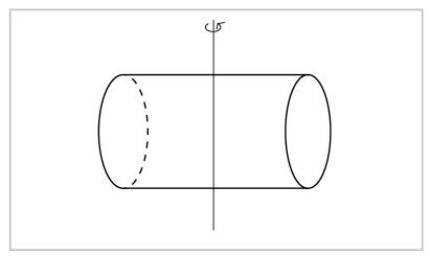
If we turn around another axis, on the contrary, we will not see the cylinder equal. We can know if someone has turned or not.
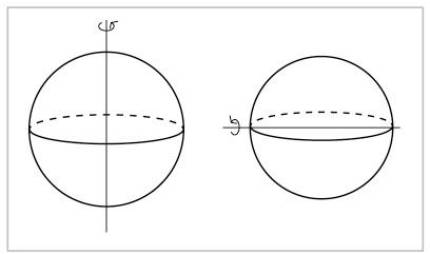
A sphere is an even more symmetrical object. Turning around any axis that passes through its center, we will see it the same.
Two types of symmetry should be mentioned: continuous symmetries and discrete symmetries. In mathematics, following means that two objects of what has been followed can be as close as you want. Therefore, in continuous symmetry, two symmetry operations are very close to each other. In the case of sphere and cylinder axes, all rotations are symmetrical, even if minimal. And there is a symmetry operation very close to a symmetry operation. In the second figure, for a rotation to be symmetrical must be 180 degrees, so very close to a symmetry rotation there is no other symmetry rotation. This symmetry is discreet.
A conservation principle tells us that the value of a physical magnitude does not vary. We have all heard of the principle of energy conservation: energy cannot be produced or destroyed. In a physical system, energy (if isolated) does not change over time. Many other conservation principles were also known. at the beginning of the 20th century: principle of conservation of the linear moment and principle of conservation of the angular moment, to mention the most important.
Physicists look for such principles because they help them better understand their systems. For example, thanks to the principle of energy conservation, we are able to explain why planets go faster on their ellipse around the sun, when they are closer to the sun than when they are further away (this principle gives an explanation to Kepler's famous law). And if that were not enough, we are able to guess the speed of the planets at one point and another. Something similar happens with atoms: we are able to know the color of light that will emit an atom of a certain chemical species, simply attending to the principle of energy conservation.
The conservation principle of the linear moment allows us to know the speed with which the objects collided after a shock will emerge. This can serve, for example, to know the speed of vehicles in a traffic accident or to control the details of the collision that created the Higgs boson.
The conservation of the angular moment has, among many others, a beautiful consequence: the orbit of a planet around the sun is in a plane. That is, a planet can never leave that plane. The plane of the Earth's orbit is called ecliptic. This word will be known to astronomers, as it is also the name of the path of the sun in the sky and the constellations of the zodiac are located in it. For if it were not for the principle of preservation of the angular moment, the orbit of the Earth would not be in the Ecliptic and would move above and below that plane leaving the plane.
XX. Some of these conservation principles were known in the early 20th century. At that time, Noether gave these principles a surprising meaning. We will state an informal version of his theorem:
“Any continuous symmetry of a system responds to a conservation principle.”
Noether contributed the demonstration of the theorem (in this article we will not give it because it is very technical). To better understand the meaning and depth of this phrase, let us take as an example the most important symmetries of physics: the symmetries of space time.
Before you start, what is a spatial time symmetry? Imagine an empty space. Interstellar space, if we want, where there is no gravity. What geometric changes can we make to this space? For example, we can make a spatial translation. That is, we can move in any direction at a certain distance. In physics there is a principle, called the principle of relativity, which tells us that all the laws of physics must be equal in this new position. If they were not the same, the result of an experiment would be different in one or another position. For example, the electrons of an atom would be placed differently in our room, in our neighbor's house, or in the Andromeda galaxy. We have never seen it that way, so we think that the laws of physics are the same at all points of space and therefore the results of all experiments are the same anywhere. That is why we say that it is a symmetry of space, because a point of space cannot be separated from all others.
The principle of relativity gives us an account of other symmetries: no one has ever seen a law of physics that changes over time. Electricity laws, for example, the XIX. They were established in the 19th century and are still identical today (called Maxwell's laws). They have not been modified. Moreover, we have powerful reasons to think that in the past there have also been several million years of laws. This phenomenon is called symmetry with temporal translations. A temporary translation for the past or for the future cannot change the law of physics. The result of an experiment will be today, yesterday or tomorrow.
So we have two symmetries that the principle of relativity has given us: spatial translations and temporal translations. There is a third symmetry that gives us the principle of relativity: symmetry with rotations. All the laws of physics are the same if we take the whole system and spin it. That is, the space does not have a privileged direction, which looks at a different physics than any other direction.
Therefore, according to the principle of relativity, space has no privileged place, no privileged moment and no privileged direction. The result of any experiment, such as the clash between two electrons or the state of three quarks forming a proton, is identical at all points of space, at all times of time and in all directions of space. If we close our eyes and make a rotation, a temporary translation or a spatial translation, in no case would it be possible to know if this operation occurred when reopening. These are the symmetries of space time that establish the principle of relativity (since the principle of relativity gives us more symmetries, but we will not mention them in this article not to confuse too much).
These three symmetries are continuous. In the case of spatial translations, we can make a very small translation and stay at a very close point. In the case of time transfers we can also “move” to a very close moment (there are no discontinuous jumps in space and time). And by choosing an axis, we can make a small rotation around it. Therefore, because of continuous symmetries, Noether's theorem can be applied.
And what would be the preserved magnitudes corresponding to these symmetries? Well, the theorem itself tells us that in the case of spatial translations, the magnitude preserved is the linear moment. In the case of time transfers, energy. And in the case of rotations, the angular moment. What a good result!
Noether discovered a profound and surprising relationship between symmetries and conservation principles: are a consequence of the other! Both go together, they cannot be separated. In a world where energy would not be preserved, the laws of physics would develop over time, that is, they would change over time. Two different moments of time would not be inseparable.
Although we have not mentioned them in this article, since we have only spoken of the symmetries of space time, this theorem is applicable to all other symmetries. To awaken the curiosity of the reader we will say that the conservation of the electric charge is also a consequence of Noether's theorem. In this case, symmetry is not spatial time, but the system of equations itself, and this more abstract symmetry is called gauge symmetry. This may include a geometric interpretation in a space of more than four dimensions. But that's a matter of leaving it for another day.
As Robert Wald said, once he has realized it, he cannot help but feel that he has learned something very deep about how nature acts. That is, therefore, the gift that this great woman left us.