Liztor beltzaren inbasioaren modelizazioa
Liztor beltzaren hedapena Europan
Zenbait iturrik espezie hau Europara 2004an sartu zela dioten arren, animalia hau 2005ean ikusi zen lehen aldiz Nérac izeneko herrian (Lot-et-Garonne-n, Frantzian) [5]. Antza denez, Asiatik ekarritako kargamentu batean iritsi zen Bordeleko portura, zeramika ekartzen zuen kontainer batean. Hortik, klimaren egokitasunak eta tokiko espezieek haiei aurre egiteko ezintasunak lagunduta, oso azkar hedatzen hasi zen eta 2009rako Frantziako 32 departamentutan detektatu zen [5].
Kontuan hartuz Iberiar penintsulako Kantauriko zonaldearen klimaren eta Frantzian liztorra ezarritako zonaldearen arteko antzekotasun bioklimatikoak, denbora kontua baino ez zen Asiako liztorrak Pirinioak gurutzatzea. Horrela, 2010eko abuztuan, Amaiur izeneko herrian (Baztan, Nafarroa) aurkitu zen mota honetako lehenengo liztorra. Geroztik, Iberiar penintsulako beste toki batzuetan agertzen joan dira, batez ere iparraldeko kostaldetik hedatuz [5].
Gaur egun, esan dezakegu Iberiar penintsulako leku askotan finkatuta dagoela intsektu hau, baina baita Europako beste herrialde askotan ere. Egoera hau larrigarria da tokiko biodibertsitatean dituen ondorioengatik, eta, bereziki, erleengan eragiten duen kalteagatik. Liztor beltzaren aurkako defentsa-mekanismo ezak erleen populazioa murriztea eragiten du, eta horrek erlezaintzan duen eraginaz gain beste hainbat kalte sortzen ditu. Izan ere, erlea loredun landareen polinizatzaile nagusia da, loreen % 70 polinizatzen baitu, eta, beraz, eragin zuzena dauka elikagaien ekoizpenean ere. Polinizazio-prozesu hori ordezkaezina izanik, izugarrizko balio ekologiko eta ekonomikoa dauka erlearen lanak [4].
Inbasioaren eredua
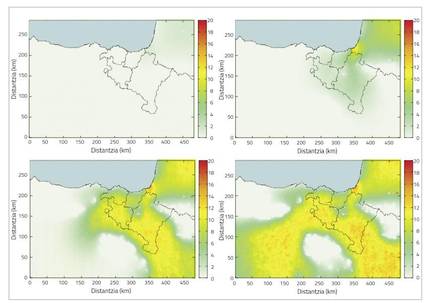
Vespa velutina populazioa oso azkar hedatzen da, eta ematen du joera bera mantenduko duela. Esan bezala, horrek arazo larria suposatzen du, bai esparru ekologikoan eta bai esparru ekonomikoan ere. Hala ere, inbasioari aurre egiteko, zenbait neurri har daitezke. Horretarako, ordea, ongi ezagutu behar dira inbasioaren ezaugarriak (abiadura, hedapena, joera…), haiekin inbasioa modelizatuko duen eredu bat sortzeko.
Populazioaren hedapenaren dinamikak, ordea, oinarrizko bi ezaugarri ditu. Lehenengoa, hedapen espaziala, populazioaren hedapenaren nolakotasuna adierazten duena. Inbasioak foku bakarra dauka, kasu honetan lehen aipatutako Bordeleko portua izango litzatekeena, eta hortik joan da hedatzen. Erraza da imajinatzea hedapen horrek likido baten joera berari jarraitu diola, eta, beraz, inbasioaren hedapen espazialak likido baten difusioaren zenbait ezaugarri izan beharko dituela. Oinarrizko bigarren ezaugarria populazioaren hazkuntza intrintsekoa da, liztor-kopuru totalari erreferentzia egiten diona. Nahiz eta Europara kolonia bakarra iritsi, gaur egun milaka eta milaka liztor-kolonia daude. Hasiera batean, hazkunde hori esponentziala den arren, beti ez da horrela. Beti horrela izango balitz liztor-kopurua handitzen eta handitzen joango litzateke, kopuru infinitu baterantz, eta jakin badakigu hori ezin dela horrela izan, ekosistema baten baliabideak mugatuak diren moduan hura osatzen duten banakoak mugatuak izan behar direlako. Errealitatean, populazioa kopuru jakin batean egonkortzen da, zeinari kapazitate maximoaren balio baiteritzo. Horrelako espezie inbaditzaileen hedapenaren dinamika hobekien azaltzen duen ekuazioari adbekzio-difusio-erreakzio ekuazio deritzo; askotan, difusio-erreakzio ekuazio ere esaten zaio. Diferentzial partzialetako ekuazio horrek ematen du une eta toki bakoitzean espezie inbaditzailearen zer populazio-dentsitate dagoen (banako-kopurua, azalera unitateko), oinarrizko bi ezaugarriak azalduz.
Noski, sistema biologikoetan izaten den moduan, sistema hau ere ezin da ziurtasun osoz aurresan; hau da, sistema indeterminista baten aurrean aurkitzen gara. Hori dela eta, gure ereduari ausazko faktore bat gehitu behar zaio. Gainera, sistema konplexu bat da, eta horrelako ekuazioak, normalean, ezin dira analitikoki ebatzi. Hori dela eta, konputazionalki ebatzi behar da eredu hau. Aztertu nahi den espazio-eremua eta denbora-tartea drisketiza daiteke, gure adbekzio-difusio-erreakzio ekuazioa drisketizatzeko, eta, gero, diferentzia finituen metodo delakoarekin, programa baten laguntzaz, inbasioa simulatzeko. Horrekin, toki eta aldiune bakoitzean dagoen Asiako liztorraren populazioaren dentsitatea lortuko da. Simulazioa egin aurretik, ordea, ekuazioaren zenbait parametro finkatu behar dira. Hortaz, Gipuzkoako Foru Aldundiak partekatutako datuak eta zenbait artikulutatik lortutako informazioa erabiliko da, zenbait hurbilketa eginez, ekuazioaren parametroak eta sistemaren xehetasunak finkatzeko [3] [1].
Aipatutakoarekin simulazioa eginez, inbasioaren hedapen espazialaren oinarrizko dinamika nahiko modu egokian azalaraztea lortzen da. Hau da, limite geologikoak errespetatzen dira (itsasoan eta itsasotik 1.000 m-tik gorako altueretan dentsitatea nulua izatea), eta hedatze-abiadura errealitatean ikusitakoarekin bat dator. Hala ere, populazioaren hazkuntzaren dinamika ez da guztiz ondo islatzen. Izan ere, gogora dezagun hainbat hurbilketa eta suposizioren bidez lortu izan direla parametro horiek, eta gerta daiteke erabilitako hurbilketa edo suposizioak guztiz egokiak ez izatea. Parametro horiek hobetzeko, ikaskuntza estatistikoa erabil daiteke.
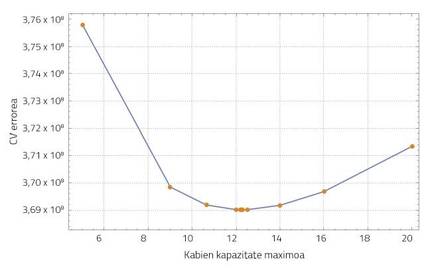
Datuak ulertzeko tresna eta teknika-multzo zabalari egiten dio erreferentzia ikaskuntza estatistikoak (ingelesez, statistical learning) [6]. Kasu honetan, kapazitate maximoaren balio egoki bat bilatzeko, baliozkotze gurutzatuaren (cross-validation, CV) metodoa erabili da. Funtsean, parametro horren balioak proposatzen joango da CV metodoa, eta, hala, konparatu egingo dira balio horiek baliatuz simulazioak Gipuzkoa osoan une ezberdinetan emandako liztorren habia-kopurua eta zonalde horretan hautemandako liztor-habien kopuruak. Simulazioaren emaitzak benetako datuetara gehien hurbiltzen dituen kapazitate maximoaren balioa izango da egokiena, CV errore txikiena duena hain zuzen. Gure sisteman, liztor beltzaren populazioaren dentsitatea 12,24 habia/km² balioan egonkortzen da.
Inbasioaren eredu egoki bat lortuta, orain, haren aurka hartu daitezkeen neurrien estrategia landu daiteke. Espezie inbaditzaile bat kontrolatzeko erabiltzen diren neurriak (kasu honetan, habiak bilatzea eta suntsitzea, gehienbat) oso garestiak izan daitezke. Hori dela eta, garrantzitsua da estrategia eraginkorrena zein den planteatzea. Helburua izaten da espeziea desagerrarazten eta ingurumenarekiko kalteak minimizatzen dituen neurriak hartzea, baina, aldi berean, ahaleginaren kostuak minimizatzea. Horretarako, kontrol-teoria izeneko matematiken esparrua erabiltzen da [2]. Estrategia optimo bat aurkitzea oso konplexua izan daiteke, baina, funtsean, kontrol-teoriaren arabera, horrelako inbasioetarako neurrien intentsitatea inbasioaren hedapenaren ertzetan bideratu behar da. Hortaz, neurriak espazioan homogeneoki aplikatu beharrean, ertzetan gogorragoak izan beharko lirateke pixkanaka-pixkanaka inbasioa “atzerantz” botatzeko eta, horrela, espeziearen aurkako kontrol-ahaleginak eraginkorragoak izateko.
Bibliografia
Idatzi zuk zeuk Gai librean atalean
Gai librean aritzeko, bidali zure artikulua aldizkaria@elhuyar.eus helbidera
Hauek dira Gai librean atalean Idazteko arauak
Gai honi buruzko eduki gehiago
Elhuyarrek garatutako teknologia









