Modelització de la invasió de vespa negra
Difusió de la vespa negra a Europa
A pesar que algunes fonts afirmen que aquesta espècie es va introduir a Europa en 2004, aquest animal es va veure per primera vegada en 2005 en Nérac (Lot-et-Garona, França) [5]. Pel que sembla, va arribar al port de Bordeus en un carregament portat des d'Àsia, en un contenidor de ceràmica. Per aquest motiu, secundat per la idoneïtat del clima i la incapacitat de les espècies locals per a combatre-les, va començar a expandir-se ràpidament i es va detectar en 32 departaments francesos per a 2009 [5].
Tenint en compte les similituds bioclimàtiques entre el clima de la zona cantàbrica de la península Ibèrica i la zona establerta per la vespa a França, l'encreuament dels Pirineus per la vespa asiàtica era només qüestió de temps. Així, a l'agost de 2010 es va trobar la primera vespa d'aquest tipus en la localitat d'Amaiur (Baztan, Navarra). Des de llavors han anat apareixent en altres llocs de la península Ibèrica, principalment en la costa nord [5].
Avui podem dir que aquest insecte està assentat en molts llocs de la península Ibèrica, però també en molts altres països europeus. Aquesta situació resulta agreujant pels seus efectes sobre la biodiversitat local i, en particular, sobre les abelles. La falta de mecanismes de defensa contra la vespa negra provoca una disminució de la població de les abelles que, a més de la seva influència en l'apicultura, genera altres danys. De fet, l'abella és el principal pol·linitzador de plantes amb flors, ja que pol·linitza el 70% de les flors, per la qual cosa també influeix directament en la producció d'aliments. Sent aquest procés de pol·linització insubstituïble, el treball de l'abella té un enorme valor ecològic i econòmic [4].
Model de la invasió
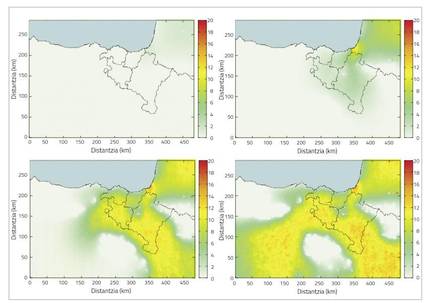
La velutina Vespa és una població que s'expandeix ràpidament i sembla que mantindrà la mateixa tendència. Com ja s'ha comentat, això suposa un greu problema tant en l'àmbit ecològic com en l'econòmic. No obstant això, per a combatre la invasió es poden prendre algunes mesures. Però per a això és necessari conèixer bé les característiques de la invasió (velocitat, extensió, tendència…) per a crear amb elles un model que modelice la invasió.
No obstant això, la dinàmica d'expansió de la població presenta dues característiques bàsiques. La primera, l'expansió espacial, que indica la naturalesa de l'expansió de la població. La invasió té un únic focus, que en aquest cas seria el port de Bordeus abans esmentat, pel qual s'ha anat expandint. És fàcil imaginar que aquesta expansió ha seguit la mateixa tendència que la d'un líquid, per la qual cosa l'expansió espacial de la invasió haurà de tenir certes característiques de la difusió d'un líquid. La segona característica bàsica és el creixement intrínsec de la població, que fa referència al nombre total de vespes. Malgrat l'arribada a Europa d'una sola colònia, en l'actualitat hi ha milers i milers de colònies de vespes. En principi, encara que aquest creixement és exponencial, no sempre és així. Si sempre fos així, el nombre de vespes s'aniria incrementant i augmentant, cap a una quantitat infinita, i sabem que això no pot ser així perquè, com els recursos d'un ecosistema són limitats, els individus que el componen han de ser limitats. En la pràctica, la població s'estabilitza en una quantitat determinada, que es considera com el valor de la capacitat màxima. L'equació que millor explica la dinàmica de propagació d'aquesta mena d'espècies invasores es diu equació d'advección-difusió-reacció, sovint també denominada equació de difusió. Aquesta equació dels diferencials parcials proporciona la densitat de població (nombre d'individus per unitat de superfície) de l'espècie invasora a cada moment i lloc, explicant les dues característiques bàsiques.
Per descomptat, igual que en els sistemes biològics, tampoc és possible predir amb certesa aquest sistema, és a dir, ens trobem davant un sistema indeterminista. Per això, al nostre model cal afegir un factor aleatori. A més, es tracta d'un sistema complex les equacions del qual normalment no poden resoldre's analíticament. Per això, aquest model ha de resoldre's computacionalment. El camp espacial i l'interval de temps que es desitja estudiar es pot drisketizar per a drisketizar la nostra equació d'advección-difusió i posteriorment, amb l'anomenat mètode de diferències finites, amb l'ajuda d'un programa, simular la invasió. Amb això s'aconsegueix la densitat de població de la vespa asiàtica present en cada lloc i moment. No obstant això, abans de realitzar la simulació és necessari fixar alguns paràmetres de l'equació. Per tant, s'utilitzaran les dades compartides per la Diputació Foral de Guipúscoa i la informació obtinguda a partir de diversos articles, fent diferents aproximacions, per a fixar els paràmetres de l'equació i els detalls del sistema [3] [1].
Simulant amb l'anterior, s'aconsegueix que la dinàmica bàsica de l'expansió espacial de la invasió aparegui d'una manera relativament adequada. És a dir, es respecten els límits geològics (densitat nul·la en la mar i a altures superiors a 1000 m de la mar) i la velocitat de propagació s'ajusta a l'observat en la realitat. No obstant això, la dinàmica de creixement de la població no es reflecteix del tot bé. Recordem que aquests paràmetres s'han obtingut a través d'aproximacions i suposicions diverses, que poden no ser del tot adequades. Per a millorar aquests paràmetres es pot utilitzar l'aprenentatge estadístic.
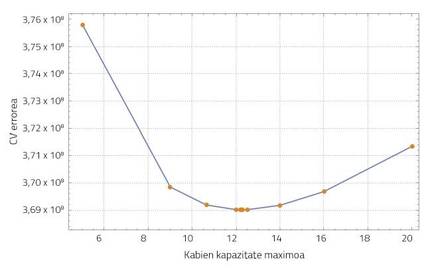
L'aprenentatge estadístic fa referència a un ampli ventall d'eines i tècniques de comprensió de dades (en anglès, statistical learning) [6]. En aquest cas s'ha utilitzat el mètode de validació creuada (cross-validation, CV) per a buscar un valor adequat de la capacitat màxima. Bàsicament, el mètode CV anirà proposant els valors d'aquest paràmetre, comparant el nombre de nius de vespes en diferents moments de la simulació en tota Guipúscoa amb el nombre de nius de vespa detectats en aquesta zona. El valor de la capacitat màxima que més acosta els resultats de la simulació a les dades reals és el més adequat, amb el menor error de CV. En el nostre sistema la densitat de població de vespa negra s'estabilitza en 12,24 nius/km².
La consecució d'un model adequat d'invasió permet ara elaborar una estratègia de mesures que puguin adoptar-se en contra seva. Les mesures que s'utilitzen per a controlar una espècie invasora, en aquest cas la cerca i destrucció de nius, poden ser molt costoses. Per això, és important plantejar quina és l'estratègia més eficaç. L'objectiu és adoptar mesures que eliminin l'espècie i minimitzin els danys al medi ambient, però alhora minimitzin els costos de l'esforç. Per a això s'utilitza el camp de les matemàtiques denominat teoria del control [2]. La cerca d'una estratègia òptima pot ser molt complexa, però en essència, segons la teoria de control, la intensitat de les mesures per a aquesta mena d'invasions ha de canalitzar-se en les vores de l'expansió de la invasió. Per tant, en lloc d'aplicar les mesures de manera homogènia en l'espai, haurien de ser més resistents en les vores per a anar a poc a poc “cap endarrere” la invasió i així poder fer més efectius els esforços de control contra l'espècie.






