Modelización de la invasión de avispa negra
Difusión de la avispa negra en Europa
A pesar de que algunas fuentes afirman que esta especie se introdujo en Europa en 2004, este animal se vio por primera vez en 2005 en Nérac (Lot-et-Garonne, Francia) [5]. Al parecer, llegó al puerto de Burdeos en un cargamento traído desde Asia, en un contenedor de cerámica. De ahí que, apoyado por la idoneidad del clima y la incapacidad de las especies locales para combatirlas, comenzó a expandirse rápidamente y se detectó en 32 departamentos franceses para 2009 [5].
Teniendo en cuenta las similitudes bioclimáticas entre el clima de la zona cantábrica de la península Ibérica y la zona establecida por la avispa en Francia, el cruce de los Pirineos por la avispa asiática era sólo cuestión de tiempo. Así, en agosto de 2010 se encontró la primera avispa de este tipo en la localidad de Amaiur (Baztan, Navarra). Desde entonces han ido apareciendo en otros lugares de la península Ibérica, principalmente en la costa norte [5].
Hoy podemos decir que este insecto está asentado en muchos lugares de la península Ibérica, pero también en otros muchos países europeos. Esta situación resulta agravante por sus efectos sobre la biodiversidad local y, en particular, sobre las abejas. La falta de mecanismos de defensa contra la avispa negra provoca una disminución de la población de las abejas que, además de su influencia en la apicultura, genera otros daños. De hecho, la abeja es el principal polinizador de plantas con flores, ya que poliniza el 70% de las flores, por lo que también influye directamente en la producción de alimentos. Siendo este proceso de polinización insustituible, el trabajo de la abeja tiene un enorme valor ecológico y económico [4].
Modelo de la invasión
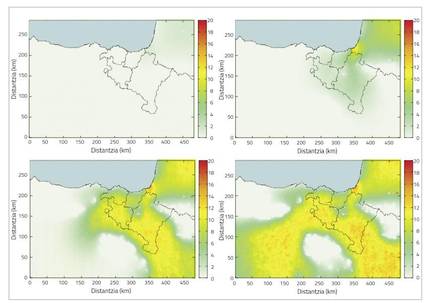
La velutina Vespa es una población que se expande rápidamente y parece que mantendrá la misma tendencia. Como ya se ha comentado, esto supone un grave problema tanto en el ámbito ecológico como en el económico. No obstante, para combatir la invasión se pueden tomar algunas medidas. Pero para ello es necesario conocer bien las características de la invasión (velocidad, extensión, tendencia…) para crear con ellas un modelo que modelice la invasión.
Sin embargo, la dinámica de expansión de la población presenta dos características básicas. La primera, la expansión espacial, que indica la naturaleza de la expansión de la población. La invasión tiene un único foco, que en este caso sería el puerto de Burdeos antes mencionado, por el que se ha ido expandiendo. Es fácil imaginar que esta expansión ha seguido la misma tendencia que la de un líquido, por lo que la expansión espacial de la invasión deberá tener ciertas características de la difusión de un líquido. La segunda característica básica es el crecimiento intrínseco de la población, que hace referencia al número total de avispas. A pesar de la llegada a Europa de una sola colonia, en la actualidad hay miles y miles de colonias de avispas. En principio, aunque este crecimiento es exponencial, no siempre es así. Si siempre fuera así, el número de avispas se iría incrementando y aumentando, hacia una cantidad infinita, y sabemos que esto no puede ser así porque, como los recursos de un ecosistema son limitados, los individuos que lo componen deben ser limitados. En la práctica, la población se estabiliza en una cantidad determinada, que se considera como el valor de la capacidad máxima. La ecuación que mejor explica la dinámica de propagación de este tipo de especies invasoras se llama ecuación de advección-difusión-reacción, a menudo también denominada ecuación de difusión. Esta ecuación de los diferenciales parciales proporciona la densidad de población (número de individuos por unidad de superficie) de la especie invasora en cada momento y lugar, explicando las dos características básicas.
Por supuesto, al igual que en los sistemas biológicos, tampoco es posible predecir con certeza este sistema, es decir, nos encontramos ante un sistema indeterminista. Por ello, a nuestro modelo hay que añadir un factor aleatorio. Además, se trata de un sistema complejo cuyas ecuaciones normalmente no pueden resolverse analíticamente. Por ello, este modelo debe resolverse computacionalmente. El campo espacial y el intervalo de tiempo que se desea estudiar se puede drisketizar para drisketizar nuestra ecuación de advección-difusión y posteriormente, con el llamado método de diferencias finitas, con la ayuda de un programa, simular la invasión. Con ello se consigue la densidad de población de la avispa asiática presente en cada lugar y momento. Sin embargo, antes de realizar la simulación es necesario fijar algunos parámetros de la ecuación. Por tanto, se utilizarán los datos compartidos por la Diputación Foral de Gipuzkoa y la información obtenida a partir de varios artículos, haciendo diferentes aproximaciones, para fijar los parámetros de la ecuación y los detalles del sistema [3] [1].
Simulando con lo anterior, se consigue que la dinámica básica de la expansión espacial de la invasión aparezca de una manera relativamente adecuada. Es decir, se respetan los límites geológicos (densidad nula en el mar y a alturas superiores a 1000 m del mar) y la velocidad de propagación se ajusta a lo observado en la realidad. Sin embargo, la dinámica de crecimiento de la población no se refleja del todo bien. Recordemos que estos parámetros se han obtenido a través de aproximaciones y suposiciones diversas, que pueden no ser del todo adecuadas. Para mejorar estos parámetros se puede utilizar el aprendizaje estadístico.
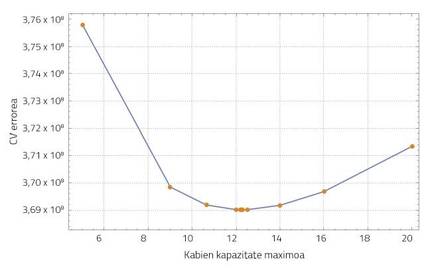
El aprendizaje estadístico hace referencia a un amplio abanico de herramientas y técnicas de comprensión de datos (en inglés, statistical learning) [6]. En este caso se ha utilizado el método de validación cruzada (cross-validation, CV) para buscar un valor adecuado de la capacidad máxima. Básicamente, el método CV irá proponiendo los valores de este parámetro, comparando el número de nidos de avispas en diferentes momentos de la simulación en toda Gipuzkoa con el número de nidos de avispa detectados en esta zona. El valor de la capacidad máxima que más acerca los resultados de la simulación a los datos reales es el más adecuado, con el menor error de CV. En nuestro sistema la densidad de población de avispa negra se estabiliza en 12,24 nidos/km².
La consecución de un modelo adecuado de invasión permite ahora elaborar una estrategia de medidas que puedan adoptarse en su contra. Las medidas que se utilizan para controlar una especie invasora, en este caso la búsqueda y destrucción de nidos, pueden ser muy costosas. Por ello, es importante plantear cuál es la estrategia más eficaz. El objetivo es adoptar medidas que eliminen la especie y minimicen los daños al medio ambiente, pero a la vez minimicen los costes del esfuerzo. Para ello se utiliza el campo de las matemáticas denominado teoría del control [2]. La búsqueda de una estrategia óptima puede ser muy compleja, pero en esencia, según la teoría de control, la intensidad de las medidas para este tipo de invasiones debe canalizarse en los bordes de la expansión de la invasión. Por lo tanto, en lugar de aplicar las medidas de forma homogénea en el espacio, deberían ser más resistentes en los bordes para ir poco a poco “hacia atrás” la invasión y así poder hacer más efectivos los esfuerzos de control contra la especie.






