Black wasp invasion modeling
Diffusion of the black wasp in Europe
Although some sources claim that this species was introduced in Europe in 2004, this animal was first seen in 2005 in Nérac (Lot-et-Garonne, France) [5]. Apparently, he arrived at the port of Bordeaux in a shipment brought from Asia, in a ceramic container. Hence, supported by the appropriateness of the climate and the inability of local species to combat them, it began to expand rapidly and was detected in 32 French departments by 2009 [5].
Taking into account the bioclimatic similarities between the climate of the Cantabrian area of the Iberian peninsula and the area established by the wasp in France, the crossing of the Pyrenees by the Asian wasp was only a matter of time. Thus, in August 2010 the first wasp of this type was found in the town of Amaiur (Baztan, Navarra). Since then they have been appearing elsewhere in the Iberian peninsula, mainly on the north coast [5].
Today we can say that this insect is located in many places of the Iberian Peninsula, but also in many other European countries. This situation is aggravated by its effects on local biodiversity and, in particular, on bees. The lack of defense mechanisms against the black wasp causes a decrease in the bee population that, in addition to its influence on beekeeping, generates other damage. In fact, the bee is the main pollinator of flowering plants, as it pollinates 70% of flowers, so it also directly influences food production. With this process of irreplaceable pollination, bee work has enormous ecological and economic value [4].
Invasion Model
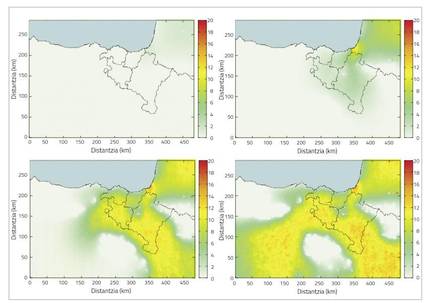
The Vespa velutina is a population that expands rapidly and seems to maintain the same trend. As already mentioned, this is a serious problem both in the ecological and economic spheres. However, some measures can be taken to combat the invasion. But for this it is necessary to know well the characteristics of the invasion (speed, extension, trend…) to create with them a model that modeling the invasion.
However, the dynamic of population expansion presents two basic characteristics. The first is spatial expansion, which indicates the nature of population expansion. The invasion has a single focus, which in this case would be the port of Bordeaux mentioned above, for which it has been expanding. It is easy to imagine that this expansion has followed the same trend as that of a liquid, so the spatial expansion of the invasion must have certain characteristics of the diffusion of a liquid. The second basic characteristic is the intrinsic growth of the population, which refers to the total number of wasps. Despite the arrival in Europe of a single colony, there are currently thousands and thousands of wasp colonies. In principle, although this growth is exponential, it is not always so. If it were always so, the number of wasps would increase and increase, towards an infinite amount, and we know that this cannot be so because, as the resources of an ecosystem are limited, the individuals that compose it must be limited. In practice, the population is stabilized in a certain amount, which is considered as the value of the maximum capacity. The equation that best explains the propagation dynamics of this type of invasive species is called advection-diffusion-reaction equation, often also called diffusion equation. This partial differential equation provides the population density (number of individuals per unit of surface) of the invasive species at each time and place, explaining the two basic characteristics.
Of course, as in biological systems, it is not possible to predict this system with certainty, that is, we are facing an indeterminist system. Therefore, to our model we must add a random factor. In addition, it is a complex system whose equations normally cannot be solved analytically. Therefore, this model must be solved computationally. The space field and time interval to be studied can be drisketized to drisketize our advection-diffusion equation and then, with the so-called finite difference method, with the help of a program, simulate invasion. This results in the population density of the Asian wasp present in each place and moment. However, before performing the simulation it is necessary to set some parameters of the equation. Therefore, the data shared by the Provincial Council of Gipuzkoa and the information obtained from several articles will be used, making different approximations, to set the parameters of the equation and the details of the system [3] [1].
Simulating the above, the basic dynamics of the invasion spatial expansion are achieved in a relatively adequate manner. That is, geological limits are respected (zero density in the sea and at heights above 1000 m of the sea) and the propagation speed is adjusted to what is observed in reality. However, the dynamic of population growth is not fully reflected. Let us remember that these parameters have been obtained through diverse approaches and assumptions, which may not be entirely appropriate. Statistical learning can be used to improve these parameters.
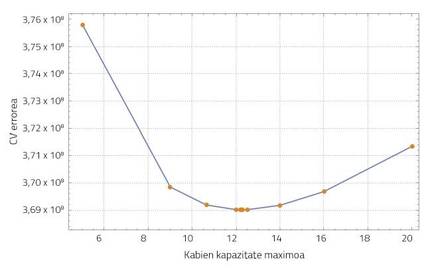
Statistical learning refers to a wide range of statistical learning tools and techniques [6]. In this case, the cross-validation (CV) method has been used to find an adequate value of the maximum capacity. Basically, the CV method will propose the values of this parameter, comparing the number of wasp nests at different times of simulation throughout Gipuzkoa with the number of wasp nests detected in this area. The maximum capacity value that most brings simulation results to real data is the most suitable, with the least CV error. In our system the black wasp population density is stabilized at 12.24 nests/km².
The achievement of an appropriate model of invasion now allows the development of a strategy of measures that can be adopted against it. The measures used to control an invasive species, in this case the search and destruction of nests, can be very expensive. Therefore, it is important to consider the most effective strategy. The objective is to adopt measures that eliminate the species and minimize damage to the environment, but at the same time minimize the costs of effort. To do this, the field of mathematics called the control theory [2] is used. The search for an optimal strategy can be very complex, but in essence, according to the control theory, the intensity of the measures for this type of invasions must be channeled at the edges of the expansion of the invasion. Therefore, instead of applying the measures homogeneously in space, they should be more resistant at the edges to gradually “back” the invasion and thus be able to make more effective control efforts against the species.






