Hasiera »   Gai librean »   Errorea "h"-z ala "h"-rik gabe?

Erro con ou sen h?

• Zabaldu:
• Twitter
• Facebook
• Emaila

Nalgúns idiomas ten son, noutro non. En euskara, aínda que estea aí cando é frío, si sente, pero non se escoita. Si o vento teno en eúscaro e, aínda que se ouza o seu verme, non se ouve "h". O erro non leva en eúscaro, pero pode levalo con matemáticas. E é que a "H" tamén ten a súa función silenciosa en matemáticas.

Aínda que nalgunhas linguas non se pronuncia, a "h" cumpre a súa función en calquera lingua, xa que una palabra non é a mesma sen "h" ou "h". Non é o mesmo coller algo (convertelo en fío) que actuar en algo; que algo sexa “cóncavo” (mancuerdas) ou que alguén sexa “contrario”. Do mesmo xeito, o erro tamén é distinto sen h ou h. Ás veces poden estar conectadas a palabra con h e sen h aínda que sexan de diferente significado. Trátase de escoitar hear en inglés e si pérdese a “h” convértese en orella, parece que perde a “h” paira non molestar o oído. O erro que se calcula en h e sen h están tamén conectados, xa que tanto uno como o outro son medidas de algo que non se realizou correctamente. Tamén é importante o lugar que ocupa a letra "H" na palabra: a función pode ser cóncava ou convexa; o neno, pola súa banda, é chinés ou alproja. A propiedade conmutativa da multiplicación fai que as matemáticas sexan indiferentes á posición que ocupa a “h” no erro, xa que depende de si existe ou non a “h”.

Estimación erro diferente

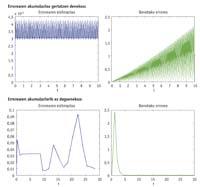
Si una ecuación diferencial non se pode resolver analiticamente, pódese resolver mediante métodos numéricos. O resultado analítico é preciso, mentres que o resultado obtido polo método numérico é aproximado e constrúese paso a paso. O erro ao soltar una ecuación diferencial por método numérico é a diferenza entre o resultado exacto e o aproximado. Un concepto que teoricamente non ten máis dificultades que una subtracción, cando hai que calculalo na práctica convértese nun concepto complexo. Pero, cal é o problema? Que descoñecemos os resultados exactos de moitas ecuacións diferenciais. Por iso, ao descoñecernos o resultado exacto, resúltanos imposible calcular o erro que estamos a cometer ao utilizar o método numérico. Aínda que non coñecemos o erro, sabemos que o resultado aproximado que se obtén utilizando métodos numéricos de orde alta é máis preciso que o obtido con métodos numéricos de orde inferior. Con todo, cada vez que se dá un paso polo método numérico, adóitase utilizar una medida que nos di si o resultado obtido nese paso é válido ou non. Que medida é este si dixemos que non se pode calcular o erro sen coñecer o resultado concreto?

A medida utilizada é a estimación do erro. Una estimación de erro de gran utilidade é a que se calcula como a diferenza de resultados que se obtén utilizando métodos numéricos de orde sucesiva, baseada na eliminación do resultado obtido mediante a utilización dun método numérico de orde ( n+1 ), que se coñece como extrapolación local. Cando a utilizamos, en cada paso esiximos que a diferenza entre os resultados obtidos por dous métodos consecutivos sexa inferior a unha tolerancia previamente establecida. Se se cumpre a condición, acéptase o resultado dado polo método de orde ( n+1 ), pola contra será necesario repetir as operacións de paso e probalo con outro paso inferior ao utilizado anteriormente. Se quixésemos utilizar extrapolación local dalgunha das medidas a realizar nun laboratorio, realizaríanse dúas medicións da cantidade que se desexa medir utilizando dous aparellos de diferente precisión. Dado que as precisións destes aparellos deben ser consecutivas, cando se dispón dun aparello de maior precisión, o segundo será o que teña maior precisión entre os aparellos de menor precisión que o primeiro. Desta maneira, asegurariamos que estamos a utilizar aparellos con precisións sucesivas. A medida debería repetirse ata que a diferenza entre ambas as medidas sexa inferior a un valor determinado e, se se cumpre a condición, aceptarase o resultado do aparello de maior precisión. Como se pode apreciar no exemplo de laboratorio, o descoñecemento do resultado real págase coa duplicación do número de cálculos.

Por tanto, a extrapolación local é un recurso seguro pero caro á vez. Dado que o seu potencial baséase na comparación dos resultados obtidos con dous métodos de diferente orde, sempre suporá un aumento do número de cálculos. Aproveitando a certeza da extrapolación local e aceptando o aumento que vai supor no número de cálculos, moitos dos creadores ou pais de métodos numéricos centráronse no deseño de métodos que podían facer que este número de cálculos non chegase a duplicarse, é dicir, tiveron como obxectivo dar a luz dous métodos de orde sucesiva coas menores diferenzas posibles. Neste sentido, mediante a utilización dun xogo de constantes diferente nunha soa operación, os métodos que realizan un método de orde n ou ( n+1 ) son moi útiles, xa que conseguen optimizar a diferenza entre dous métodos de orde sucesiva. Exemplo diso son os métodos Runge-Kutta introducidos. Nelas, abonda con que, ademais das operacións realizadas paira obter o resultado polo método de orde ( n+1 ), realícese una única operación paira obter o resultado que nos proporciona o método de orde n. Ofrecen, por tanto, una opción económica paira obter resultados de diferentes ordes. Só hai outra opción máis económica que a de conseguir ambas as ao prezo dunha. Pero iso é imposible, porque haberá que diferenciar os diferentes métodos en algo.

Estimación con h sen h

Nos métodos numéricos, a letra "h" utilízase paira indicar o tamaño do paso. Coñecido o resultado exacto do punto inicial, dáse un paso de tamaño "h" no que se calcula o resultado aproximado da ecuación diferencial mediante as operacións que o método numérico esíxenos. Utilizando o resultado aproximado obtido no novo punto repítese o proceso. Paira medir o erro en cada paso adóitanse utilizar estimacións de dous tipos: una, denominada estimación por unidade de paso, diferenza pura entre os resultados obtidos por métodos consecutivos (sen h); e outra, denominada estimación por paso, que se obtén multiplicando a diferenza entre os resultados polo tamaño do paso (“h”). Por suposto, a estimación con h e sen h non son iguais. Supoñamos que temos una estimación do erro por unidade de paso. Dado que os tamaños dos pasos que se utilizan habitualmente son menores que a unidade, a estimación que se obtén multiplicando esta estimación por “h” é menor que a que temos previamente. En consecuencia, pode suceder que una estimación non inferior á tolerancia establecida sen multiplicar por “h”, despois de multiplicar por “h”, por baixo da tolerancia, é dicir, que a pequeñez do paso axudou a pasar a barreira. Ademais, a estimación multiplicada por “h” dá una vantaxe especial aos pasos pequenos, xa que ao multiplicar a estimación por unha “h” menor, a nova estimación será menor. Noutras palabras, a estimación por unidade de paso (sen h) coloca a barreira á mesma altura. A estimación que se obtén multiplicando por “H” baixa a barreira a todos os pasos. Os pasos máis reducidos son os pequenos.

Ás veces, o descenso da barreira non se verá afectado, xa que haberá estimacións que pasarían sen axuda a altura inicial da barreira. Pero haberá saltos que non poden superar a altura inicial da barreira e que se verán afectados o descenso da barreira. En consecuencia, o paso que debería repetirse utilizando outra estimación considerarase válido. A repetición dun paso supón probar con pasos máis pequenos, e se os pasos son pequenos, necesítase máis. Por tanto, cando utilizamos as estimacións nas que estamos a baixar a barreira, daranse menos pasos e por tanto maiores que nas que non baixan. A moeda, con todo, ten outro aspecto, xa que pode ocorrer que o descenso da barreira non teña o resultado desexado. Isto pode influír negativamente no erro final e reducir drasticamente a calidade do resultado aproximado que obtemos. En xeral, a estimación que se calcula sen h levará a necesidade de dar pasos máis pequenos, pero a acumulación de erro real tamén será menor.

Estimación erro en h ou sen h

As ecuacións diferenciais poden ser ríxidas ou non ríxidas. A definición práctica da ecuación diferencial ríxida é a dunha ecuación que debe dar moitos pasos a un algoritmo. Aínda que a palabra "moito" non indica números concretos, 100 pasos non son moitos e 3.000 son moitos. Cando o problema é ríxido, prefírese utilizar una estimación sen “h”, xa que coa estimación con “h” obterase un resultado moito mellor que o que se obtería coa estimación sen “h”. Aínda que o problema non sexa ríxido, o resultado obtido cunha estimación sen h será, na maioría dos casos, mellor que o obtido con h, pero o resultado --diferencia entre ambos - non será tan espectacular, é dicir, o traballo adicional que supón a utilización dunha estimación sen h en ecuacións diferenciais non ríxidas non xerará moito brillo na solución.

Nos idiomas é habitual que una palabra perda ou gañe a "h" segundo a época. Exemplos diso son a construción de muros ás veces con ou sen h, ou a curación de pacientes en hospitais con ou sen h. Con todo, a función ou significado das palabras que se pegaron ou eliminado a “h” pola época seguiu sendo a mesma. O tema dos erros con h e sen h en matemáticas non depende da época: sempre estivo a convivencia entre ambos, e ambos son necesarios porque a función dun e outro nunca foi a mesma. Do mesmo xeito que consultamos no dicionario se una palabra ten ou non una “h”, paira decidir si utiliza ou non una “h” na estimación do erro haberá que “consultar” o problema a liberar, xa que a clave do éxito que obteremos no resultado será que a estimación do erro teña ou non una “h”.