Hasiera »   Gai librean »   Errorea "h"-z ala "h"-rik gabe?

¿Error con o sin h?

• Zabaldu:
• Twitter
• Facebook
• Emaila

En algunos idiomas tiene sonido, en otros no. En euskara, aunque esté ahí cuando es frío, sí se siente, pero no se escucha. Si el viento lo tiene en euskera y, aunque se oiga su gusano, no se oye "h". El error no lleva en euskera, pero puede llevarlo con matemáticas. Y es que la "H" también tiene su función silenciosa en matemáticas.

Aunque en algunas lenguas no se pronuncia, la "h" cumple su función en cualquier lengua, ya que una palabra no es la misma sin "h" o "h". No es lo mismo coger algo (convertirlo en hilo) que actuar en algo; que algo sea “cóncavo” (mancuerdas) o que alguien sea “contrario”. Del mismo modo, el error también es distinto sin h o h. A veces pueden estar conectadas la palabra con h y sin h aunque sean de diferente significado. Se trata de escuchar hear en inglés y si se pierde la “h” se convierte en oreja, parece que pierde la “h” para no molestar el oído. El error que se calcula en h y sin h están también conectados, ya que tanto uno como el otro son medidas de algo que no se ha realizado correctamente. También es importante el lugar que ocupa la letra "H" en la palabra: la función puede ser cóncava o convexa; el niño, por su parte, es chino o alproja. La propiedad conmutativa de la multiplicación hace que las matemáticas sean indiferentes a la posición que ocupa la “h” en el error, ya que depende de si existe o no la “h”.

Estimación error diferente

Si una ecuación diferencial no se puede resolver analíticamente, se puede resolver mediante métodos numéricos. El resultado analítico es preciso, mientras que el resultado obtenido por el método numérico es aproximado y se construye paso a paso. El error al soltar una ecuación diferencial por método numérico es la diferencia entre el resultado exacto y el aproximado. Un concepto que teóricamente no tiene más dificultades que una sustracción, cuando hay que calcularlo en la práctica se convierte en un concepto complejo. Pero, ¿cuál es el problema? Que desconocemos los resultados exactos de muchas ecuaciones diferenciales. Por ello, al desconocernos el resultado exacto, nos resulta imposible calcular el error que estamos cometiendo al utilizar el método numérico. Aunque no conocemos el error, sabemos que el resultado aproximado que se obtiene utilizando métodos numéricos de orden alto es más preciso que el obtenido con métodos numéricos de orden inferior. Sin embargo, cada vez que se da un paso por el método numérico, se suele utilizar una medida que nos dice si el resultado obtenido en ese paso es válido o no. ¿Qué medida es esta si hemos dicho que no se puede calcular el error sin conocer el resultado concreto?

La medida utilizada es la estimación del error. Una estimación de error de gran utilidad es la que se calcula como la diferencia de resultados que se obtiene utilizando métodos numéricos de orden sucesivo, basada en la eliminación del resultado obtenido mediante la utilización de un método numérico de orden ( n+1 ), que se conoce como extrapolación local. Cuando la utilizamos, en cada paso exigimos que la diferencia entre los resultados obtenidos por dos métodos consecutivos sea inferior a una tolerancia previamente establecida. Si se cumple la condición, se acepta el resultado dado por el método de orden ( n+1 ), de lo contrario será necesario repetir las operaciones de paso y probarlo con otro paso inferior al utilizado anteriormente. Si quisiéramos utilizar extrapolación local de alguna de las medidas a realizar en un laboratorio, se realizarían dos mediciones de la cantidad que se desea medir utilizando dos aparatos de diferente precisión. Dado que las precisiones de estos aparatos deben ser consecutivas, cuando se dispone de un aparato de mayor precisión, el segundo será el que tenga mayor precisión entre los aparatos de menor precisión que el primero. De esta manera, aseguraríamos que estamos utilizando aparatos con precisiones sucesivas. La medida debería repetirse hasta que la diferencia entre ambas medidas sea inferior a un valor determinado y, si se cumple la condición, se aceptará el resultado del aparato de mayor precisión. Como se puede apreciar en el ejemplo de laboratorio, el desconocimiento del resultado real se paga con la duplicación del número de cálculos.

Por tanto, la extrapolación local es un recurso seguro pero caro a la vez. Dado que su potencial se basa en la comparación de los resultados obtenidos con dos métodos de diferente orden, siempre supondrá un aumento del número de cálculos. Aprovechando la certeza de la extrapolación local y aceptando el aumento que va a suponer en el número de cálculos, muchos de los creadores o padres de métodos numéricos se han centrado en el diseño de métodos que podían hacer que este número de cálculos no llegara a duplicarse, es decir, han tenido como objetivo dar a luz dos métodos de orden sucesivo con las menores diferencias posibles. En este sentido, mediante la utilización de un juego de constantes diferente en una sola operación, los métodos que realizan un método de orden n o ( n+1 ) son muy útiles, ya que consiguen optimizar la diferencia entre dos métodos de orden sucesivo. Ejemplo de ello son los métodos Runge-Kutta introducidos. En ellas, basta con que, además de las operaciones realizadas para obtener el resultado por el método de orden ( n+1 ), se realice una única operación para obtener el resultado que nos proporciona el método de orden n. Ofrecen, por tanto, una opción económica para obtener resultados de diferentes órdenes. Sólo hay otra opción más económica que la de conseguir ambas al precio de una. Pero eso es imposible, porque habrá que diferenciar los diferentes métodos en algo.

Estimación con h sin h

En los métodos numéricos, la letra "h" se utiliza para indicar el tamaño del paso. Conocido el resultado exacto del punto inicial, se da un paso de tamaño "h" en el que se calcula el resultado aproximado de la ecuación diferencial mediante las operaciones que el método numérico nos exige. Utilizando el resultado aproximado obtenido en el nuevo punto se repite el proceso. Para medir el error en cada paso se suelen utilizar estimaciones de dos tipos: una, denominada estimación por unidad de paso, diferencia pura entre los resultados obtenidos por métodos consecutivos (sin h); y otra, denominada estimación por paso, que se obtiene multiplicando la diferencia entre los resultados por el tamaño del paso (“h”). Por supuesto, la estimación con h y sin h no son iguales. Supongamos que tenemos una estimación del error por unidad de paso. Dado que los tamaños de los pasos que se utilizan habitualmente son menores que la unidad, la estimación que se obtiene multiplicando esta estimación por “h” es menor que la que tenemos previamente. En consecuencia, puede suceder que una estimación no inferior a la tolerancia establecida sin multiplicar por “h”, después de multiplicar por “h”, por debajo de la tolerancia, es decir, que la pequeñez del paso ha ayudado a pasar la barrera. Además, la estimación multiplicada por “h” da una ventaja especial a los pasos pequeños, ya que al multiplicar la estimación por una “h” menor, la nueva estimación será menor. En otras palabras, la estimación por unidad de paso (sin h) coloca la barrera a la misma altura. La estimación que se obtiene multiplicando por “H” baja la barrera a todos los pasos. Los pasos más reducidos son los pequeños.

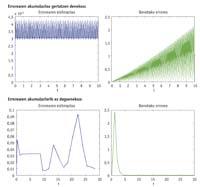
A veces, el descenso de la barrera no se verá afectado, ya que habrá estimaciones que pasarían sin ayuda la altura inicial de la barrera. Pero habrá saltos que no pueden superar la altura inicial de la barrera y que se verán afectados por el descenso de la barrera. En consecuencia, el paso que debería repetirse utilizando otra estimación se considerará válido. La repetición de un paso supone probar con pasos más pequeños, y si los pasos son pequeños, se necesita más. Por lo tanto, cuando utilizamos las estimaciones en las que estamos bajando la barrera, se darán menos pasos y por lo tanto mayores que en las que no bajan. La moneda, sin embargo, tiene otro aspecto, ya que puede ocurrir que el descenso de la barrera no tenga el resultado deseado. Esto puede influir negativamente en el error final y reducir drásticamente la calidad del resultado aproximado que obtenemos. En general, la estimación que se calcula sin h conllevará la necesidad de dar pasos más pequeños, pero la acumulación de error real también será menor.

Estimación error en h o sin h

Las ecuaciones diferenciales pueden ser rígidas o no rígidas. La definición práctica de la ecuación diferencial rígida es la de una ecuación que debe dar muchos pasos a un algoritmo. Aunque la palabra "mucho" no indica números concretos, 100 pasos no son muchos y 3.000 son muchos. Cuando el problema es rígido, se prefiere utilizar una estimación sin “h”, ya que con la estimación con “h” se obtendrá un resultado mucho mejor que el que se obtendría con la estimación sin “h”. Aunque el problema no sea rígido, el resultado obtenido con una estimación sin h será, en la mayoría de los casos, mejor que el obtenido con h, pero el resultado --diferencia entre ambos - no será tan espectacular, es decir, el trabajo adicional que supone la utilización de una estimación sin h en ecuaciones diferenciales no rígidas no generará mucho brillo en la solución.

En los idiomas es habitual que una palabra pierda o gane la "h" según la época. Ejemplos de ello son la construcción de muros a veces con o sin h, o la curación de pacientes en hospitales con o sin h. Sin embargo, la función o significado de las palabras que se han pegado o eliminado la “h” por la época ha seguido siendo la misma. El tema de los errores con h y sin h en matemáticas no depende de la época: siempre ha estado la convivencia entre ambos, y ambos son necesarios porque la función de uno y otro nunca ha sido la misma. Al igual que consultamos en el diccionario si una palabra tiene o no una “h”, para decidir si utiliza o no una “h” en la estimación del error habrá que “consultar” el problema a liberar, ya que la clave del éxito que obtendremos en el resultado será que la estimación del error tenga o no una “h”.