Hasiera »   Gai librean »   Errorea "h"-z ala "h"-rik gabe?

Erreur avec ou sans h ?

• Zabaldu:
• Twitter
• Facebook
• Emaila

Dans certaines langues, il a du son, dans d'autres pas. En basque, même s'il est là quand il fait froid, il se sent, mais on n'écoute pas. Si le vent l'a en basque et, même si son ver est entendu, on n'entend pas "h". L'erreur ne porte pas en euskera, mais vous pouvez le porter avec des mathématiques. Et c'est que le "H" a aussi sa fonction silencieuse en mathématiques.

Bien que dans certaines langues il ne soit pas prononcé, le "h" remplit sa fonction dans n'importe quelle langue, car un mot n'est pas le même sans "h" ou "h". Ce n’est pas la même chose de prendre quelque chose (le transformer en fil) que d’agir en quelque chose ; que quelque chose soit « concave » (mancordes) ou que quelqu’un soit « contraire ». De même, l'erreur est également différente sans h ou h. Parfois, le mot peut être connecté avec h et sans h même s'ils ont une signification différente. Il s'agit d'entendre hear en anglais et si vous perdez le “h” devient oreille, il semble que vous perdez le “h” pour ne pas déranger l'oreille. L'erreur calculée en h et sans h sont également connectés, car l'un comme l'autre sont des mesures de quelque chose qui n'a pas été fait correctement. Il est également important de placer la lettre "H" dans le mot: la fonction peut être concave ou convexe; l'enfant, quant à lui, est chinois ou alproja. La propriété commutative de la multiplication rend les mathématiques indifférentes à la position occupée par le «h» dans l'erreur, car elle dépend de si le «h» existe ou non.

Estimation erreur différente

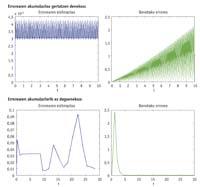
Si une équation différentielle ne peut pas être résolue de manière analytique, elle peut être résolue par des méthodes numériques. Le résultat analytique est précis, tandis que le résultat obtenu par la méthode numérique est approximatif et se construit pas à pas. L'erreur lors du relâchement d'une équation différentielle par méthode numérique est la différence entre le résultat exact et approximatif. Un concept qui théoriquement n'a pas plus de difficultés qu'une soustraction, quand il faut le calculer dans la pratique devient un concept complexe. Mais quel est le problème? Nous ne connaissons pas les résultats exacts de nombreuses équations différentielles. Par conséquent, en ignorant le résultat exact, il nous est impossible de calculer l'erreur que nous commettons en utilisant la méthode numérique. Bien que nous ne connaissions pas l'erreur, nous savons que le résultat approximatif obtenu en utilisant des méthodes numériques d'ordre élevé est plus précis que celui obtenu par des méthodes numériques d'ordre inférieur. Cependant, chaque fois qu'une étape est franchie par la méthode numérique, une mesure nous indique généralement si le résultat obtenu à cette étape est valide ou non. Quelle est cette mesure si nous avons dit que l'erreur ne peut pas être calculée sans connaître le résultat concret?

La mesure utilisée est l'estimation de l'erreur. Une estimation d'erreur de grande utilité est celle qui est calculée comme la différence de résultats obtenue en utilisant des méthodes numériques d'ordre successif, basée sur l'élimination du résultat obtenu en utilisant une méthode numérique d'ordre ( n+1 ), qui est connue comme extrapolation locale. Lorsque nous l'utilisons, nous exigeons à chaque étape que la différence entre les résultats obtenus par deux méthodes consécutives soit inférieure à une tolérance préalablement établie. Si la condition est remplie, le résultat donné par la méthode de commande ( n+1 ) est accepté, sinon il faudra répéter les opérations de passage et le tester avec une autre étape inférieure à celle utilisée précédemment. Si nous voulons utiliser l'extrapolation locale de l'une des mesures à effectuer dans un laboratoire, deux mesures de la quantité à mesurer seraient effectuées à l'aide de deux appareils de précision différente. Étant donné que les précisions de ces appareils doivent être consécutives, lorsqu'un appareil de plus grande précision est disponible, le second est celui qui a une plus grande précision parmi les appareils de moindre précision que le premier. De cette façon, nous assurerions que nous utilisons des appareils avec des précisions successives. La mesure doit être répétée jusqu'à ce que la différence entre les deux mesures soit inférieure à une valeur donnée et, si la condition est remplie, le résultat de l'appareil le plus précis sera accepté. Comme on peut l'apprécier dans l'exemple de laboratoire, la méconnaissance du résultat réel est payée avec la duplication du nombre de calculs.

Par conséquent, l'extrapolation locale est une ressource sûre mais chère à la fois. Comme son potentiel est basé sur la comparaison des résultats obtenus avec deux méthodes d'ordre différent, il entraînera toujours une augmentation du nombre de calculs. Profitant de la certitude de l'extrapolation locale et en acceptant l'augmentation qui va supposer dans le nombre de calculs, de nombreux créateurs ou parents de méthodes numériques se sont concentrés sur la conception de méthodes qui pourraient faire ce nombre de calculs ne pas doubler, c'est-à-dire ont eu pour objectif de donner naissance à deux méthodes d'ordre successif avec les moindres différences possibles. En ce sens, en utilisant un jeu de constantes différent en une seule opération, les méthodes qui réalisent une méthode d'ordre n ou ( n+1 ) sont très utiles car elles permettent d'optimiser la différence entre deux méthodes d'ordre successif. Les méthodes Runge-Kutta introduites en sont un exemple. Il suffit, en plus des opérations effectuées pour obtenir le résultat par la méthode de commande ( n+1 ), d'effectuer une seule opération pour obtenir le résultat que nous fournit la méthode de commande n. Ils offrent donc une option économique pour obtenir des résultats de différents ordres. Il n'y a qu'une autre option plus économique que celle d'obtenir les deux au prix d'une. Mais cela est impossible, car il faudra différencier les différentes méthodes en quelque chose.

Estimation avec h sans h

Dans les méthodes numériques, la lettre "h" est utilisée pour indiquer la taille de l'étape. Le résultat exact du point de départ est connu, un pas de taille "h" dans lequel le résultat approximatif de l'équation différentielle est calculé par les opérations que la méthode numérique exige. En utilisant le résultat approximatif obtenu dans le nouveau point, le processus est répété. Pour mesurer l'erreur à chaque étape, on utilise généralement des estimations de deux types: une, appelée estimation par unité de passage, différence pure entre les résultats obtenus par des méthodes consécutives (sans h); et une autre, appelée estimation par étape, qui est obtenue en multipliant la différence entre les résultats par la taille de l'étape (“h”). Naturellement, l'évaluation avec h et sans h ne sont pas identiques. Supposons que nous ayons une estimation de l'erreur par unité de passage. Étant donné que la taille des étapes habituellement utilisées est inférieure à l’unité, l’estimation obtenue en multipliant cette estimation par “h” est inférieure à celle que nous avons précédemment. En conséquence, il peut arriver qu’une estimation non inférieure à la tolérance établie sans multiplier par «h», après la multiplication par «h», en dessous de la tolérance, c’est-à-dire que la petitesse du passage a aidé à passer la barrière. De plus, l’estimation multipliée par “h” donne un avantage particulier aux petites étapes, car en multipliant l’estimation par “h” mineur, la nouvelle estimation sera moindre. En d'autres termes, l'estimation par unité de passage (sans h) place la barrière à la même hauteur. L’estimation obtenue en multipliant par “H” abaisse la barrière à toutes les étapes. Les étapes les plus réduites sont les plus petites.

Parfois, la descente de la barrière ne sera pas affectée, car il y aura des estimations qui passeraient sans aide la hauteur initiale de la barrière. Mais il y aura des sauts qui ne peuvent pas dépasser la hauteur initiale de la barrière et qui seront affectés par la descente de la barrière. Par conséquent, l'étape à répéter en utilisant une autre estimation sera considérée comme valide. La répétition d'une étape implique d'essayer avec des étapes plus petites, et si les étapes sont petites, il faut plus. Par conséquent, lorsque nous utilisons les estimations où nous abaissons la barrière, il y aura moins d'étapes et donc plus grandes que celles qui ne descendent pas. La monnaie, cependant, a un autre aspect, car il peut arriver que la descente de la barrière n'ait pas le résultat souhaité. Cela peut influencer négativement l'erreur finale et réduire considérablement la qualité du résultat approximatif que nous obtenons. En général, l'estimation calculée sans h entraînera la nécessité de prendre des mesures plus petites, mais l'accumulation d'erreur réelle sera également inférieure.

Estimation erreur en h ou sans h

Les équations différentielles peuvent être rigides ou non rigides. La définition pratique de l'équation différentielle rigide est celle d'une équation qui doit prendre de nombreuses étapes à un algorithme. Bien que le mot «beaucoup» n'indique pas de chiffres concrets, 100 étapes ne sont pas nombreux et 3000 sont nombreux. Lorsque le problème est rigide, on préfère utiliser une estimation sans “h”, car avec l’estimation avec “h” on obtiendra un résultat beaucoup mieux que celui obtenu avec l’estimation sans “h”. Bien que le problème ne soit pas rigide, le résultat obtenu avec une estimation sans h sera, dans la plupart des cas, mieux que celui obtenu avec h, mais le résultat --différence entre les deux - ne sera pas si spectaculaire, c'est-à-dire le travail supplémentaire qui suppose l'utilisation d'une estimation sans h dans des équations différentielles non rigides ne produira pas beaucoup de luminosité dans la solution.

Dans les langues, il est courant qu'un mot perde ou gagne le "h" selon l'époque. Exemples sont la construction de murs parfois avec ou sans h, ou la guérison des patients dans les hôpitaux avec ou sans h. Cependant, la fonction ou la signification des mots qui ont collé ou supprimé le “h” par le temps est resté le même. Le sujet des erreurs avec h et sans h en mathématiques ne dépend pas de l'époque: il a toujours été la coexistence entre les deux, et les deux sont nécessaires parce que la fonction de l'un et l'autre n'a jamais été la même. Tout comme nous consultons dans le dictionnaire si un mot a ou non un « h », pour décider s’il utilise ou non un « h » dans l’estimation de l’erreur, il faudra « consulter » le problème à libérer, car la clé du succès que nous obtiendrons dans le résultat sera que l’estimation de l’erreur ait ou non un « h ».