Error amb o sense h?

Estimació error diferent
Si una equació diferencial no es pot resoldre analíticament, es pot resoldre mitjançant mètodes numèrics. El resultat analític cal, mentre que el resultat obtingut pel mètode numèric és aproximat i es construeix pas a pas. L'error en deixar anar una equació diferencial per mètode numèric és la diferència entre el resultat exacte i l'aproximat. Un concepte que teòricament no té més dificultats que una sostracció, quan cal calcular-lo en la pràctica es converteix en un concepte complex. Però, quin és el problema? Que desconeixem els resultats exactes de moltes equacions diferencials. Per això, en desconèixer-nos el resultat exacte, ens resulta impossible calcular l'error que estem cometent en utilitzar el mètode numèric. Encara que no coneixem l'error, sabem que el resultat aproximat que s'obté utilitzant mètodes numèrics d'ordre alt és més precís que l'obtingut amb mètodes numèrics d'ordre inferior. No obstant això, cada vegada que es fa un pas pel mètode numèric, se sol utilitzar una mesura que ens diu si el resultat obtingut en aquest pas és vàlid o no. Quina mesura és aquesta si hem dit que no es pot calcular l'error sense conèixer el resultat concret?
La mesura utilitzada és l'estimació de l'error. Una estimació d'error de gran utilitat és la que es calcula com la diferència de resultats que s'obté utilitzant mètodes numèrics d'ordre successiu, basada en l'eliminació del resultat obtingut mitjançant la utilització d'un mètode numèric d'ordre ( n+1 ), que es coneix com a extrapolació local. Quan la utilitzem, en cada pas exigim que la diferència entre els resultats obtinguts per dos mètodes consecutius sigui inferior a una tolerància prèviament establerta. Si es compleix la condició, s'accepta el resultat donat pel mètode d'ordre ( n+1 ), en cas contrari serà necessari repetir les operacions de pas i provar-ho amb un altre pas inferior a l'utilitzat anteriorment. Si volguéssim utilitzar extrapolació local d'alguna de les mesures a realitzar en un laboratori, es realitzarien dos mesuraments de la quantitat que es desitja mesurar utilitzant dos aparells de diferent precisió. Atès que les precisions d'aquests aparells han de ser consecutives, quan es disposa d'un aparell de major precisió, el segon serà el que tingui major precisió entre els aparells de menor precisió que el primer. D'aquesta manera, asseguraríem que estem utilitzant aparells amb precisions successives. La mesura hauria de repetir-se fins que la diferència entre totes dues mesures sigui inferior a un valor determinat i, si es compleix la condició, s'acceptarà el resultat de l'aparell de major precisió. Com es pot apreciar en l'exemple de laboratori, el desconeixement del resultat real es paga amb la duplicació del nombre de càlculs.

Per tant, l'extrapolació local és un recurs segur però car alhora. Atès que el seu potencial es basa en la comparació dels resultats obtinguts amb dos mètodes de diferent ordre, sempre suposarà un augment del nombre de càlculs. Aprofitant la certesa de l'extrapolació local i acceptant l'augment que suposarà en el nombre de càlculs, molts dels creadors o pares de mètodes numèrics s'han centrat en el disseny de mètodes que podien fer que aquest nombre de càlculs no arribés a duplicar-se, és a dir, han tingut com a objectiu donar a llum dos mètodes d'ordre successiu amb les menors diferències possibles. En aquest sentit, mitjançant la utilització d'un joc de constants diferent en una sola operació, els mètodes que realitzen un mètode d'ordre n o ( n+1 ) són molt útils, ja que aconsegueixen optimitzar la diferència entre dos mètodes d'ordre successiu. Exemple d'això són els mètodes Runge-Kutta introduïts. En elles, n'hi ha prou que, a més de les operacions realitzades per a obtenir el resultat pel mètode d'ordre ( n+1 ), es realitzi una única operació per a obtenir el resultat que ens proporciona el mètode d'ordre n. Ofereixen, per tant, una opció econòmica per a obtenir resultats de diferents ordres. Només hi ha una altra opció més econòmica que la d'aconseguir totes dues al preu d'una. Però això és impossible, perquè caldrà diferenciar els diferents mètodes en alguna cosa.
Estimació amb h sense h

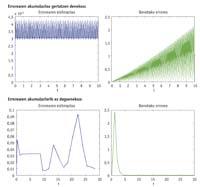
A vegades, el descens de la barrera no es veurà afectat, ja que hi haurà estimacions que passarien sense ajuda l'altura inicial de la barrera. Però hi haurà salts que no poden superar l'altura inicial de la barrera i que es veuran afectats pel descens de la barrera. En conseqüència, el pas que hauria de repetir-se utilitzant una altra estimació es considerarà vàlid. La repetició d'un pas suposa provar amb passos més petits, i si els passos són petits, es necessita més. Per tant, quan utilitzem les estimacions en les quals estem baixant la barrera, es faran menys passos i per tant majors que en les quals no baixen. La moneda, no obstant això, té un altre aspecte, ja que pot ocórrer que el descens de la barrera no tingui el resultat desitjat. Això pot influir negativament en l'error final i reduir dràsticament la qualitat del resultat aproximat que obtenim. En general, l'estimació que es calcula sense h comportarà la necessitat de fer passos més petits, però l'acumulació d'error real també serà menor.

Estimació error en h o sense h
Les equacions diferencials poden ser rígides o no rígides. La definició pràctica de l'equació diferencial rígida és la d'una equació que ha de fer molts passos a un algorisme. Encara que la paraula "molt" no indica números concrets, 100 passos no són molts i 3.000 són molts. Quan el problema és rígid, es prefereix utilitzar una estimació sense “h”, ja que amb l'estimació amb “h” s'obtindrà un resultat molt millor que el que s'obtindria amb l'estimació sense “h”. Encara que el problema no sigui rígid, el resultat obtingut amb una estimació sense h serà, en la majoria dels casos, millor que l'obtingut amb h, però el resultat --diferencia entre tots dos - no serà tan espectacular, és a dir, el treball addicional que suposa la utilització d'una estimació sense h en equacions diferencials no rígides no generarà molta lluentor en la solució.

En els idiomes és habitual que una paraula perdi o guanyi la h "" segons l'època. Exemples d'això són la construcció de murs a vegades amb o sense h, o la curació de pacients en hospitals amb o sense h. No obstant això, la funció o significat de les paraules que s'han pegat o eliminat la “h” per l'època ha continuat sent la mateixa. El tema dels errors amb h i sense h en matemàtiques no depèn de l'època: sempre ha estat la convivència entre tots dos, i tots dos són necessaris perquè la funció de l'un i l'altre mai ha estat la mateixa. Igual que consultem en el diccionari si una paraula té o no una “h”, per a decidir si utilitza o no una “h” en l'estimació de l'error caldrà “consultar” el problema a alliberar, ja que la clau de l'èxit que obtindrem en el resultat serà que l'estimació de l'error tingui o no una “h”.






