Probas do teorema de Pitágoras
Con este nome coñécese o resultado correspondente a triángulos rectos, é dicir, a suma de cadrados dos catetos é o cadrado da hipotenusa. Antes de Pitágoras era coñecido noutros países como Exipto, Babilonia, China, etc. (Os europeos, como sempre, nosa propio sopapo).
Sabemos que Pitágoras viaxou a Exipto e Babilonia, e quizais á India. Naquelas longas viaxes, ademais dos descubrimentos relixiosos e astronómicos, tamén adquiriu numerosos descubrimentos matemáticos (Por certo, Pitágoras foi contemporáneo de Buda, Confucio e Lao Ts).
Adóitase recoñecer que a ciencia e as matemáticas anteriores ás de Helena eran, en xeral, útiles. Con todo, algúns indicios suxírennos que se fixo un estudo propio das matemáticas. Nun texto cuneiforme da Universidade de Yale aparece un cadrado e as súas diagonais. Xunto a un lado pódense ver os números 30 e 42;25,35 e 1;24,51,10 (os números están representados no sistema sexagesimal).
O último número é a relación entre a diagonal e as lonxitudes ao lado, e está máis preto de - 2 que o millón. Este nivel de precisión débese ao coñecemento do teorema de Pitágoras. O descubrimento do teorema de Pitágoras non se limitaba aos triángulos isósceles. Por exemplo, nun antigo problema colócase una escaleira de 0;30 de lonxitude contra un muro e pregúntase: canto se afastará da base do muro o extremo inferior da escaleira, se o extremo superior baixa 0;6 unidades?.
Os babilonios xa coñecían o teorema. Paira xustificar o nome díxose que o teorema de Pitágoras foi probado primeiro polos pitagóricos, pero iso non se pode comprobar porque non hai probas.
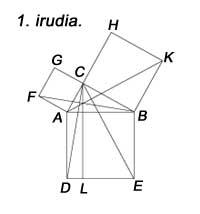
Non de Pitágoras, pero coñecemos outras probas. O primeiro libro de Euklides conclúe coas propostas 47 e 48, nas que se mostran as probas do teorema de Pitágoras e a súa inversa. Euklides evitou o uso de proporcións na demostración debido ás dificultades que podía xerar a malversación. Con todo, Euklides, utilizando a figura 1, realizou una demostración elegante. A demostración obtense: O cadrado que se constrúe sobre o lado AC é o dobre do triángulo FAB ou o dobre do triángulo CAD, que é igual ao rectángulo Ao. Por outra banda, o cadrado sobre o lado BC é o dobre do triángulo ABK ou o dobre do triángulo BCE, é dicir, igual ao rectángulo BL. En consecuencia, a suma de cadrados é igual á suma de rectángulos, é dicir, o cadrado AB.
O mérito de Euklides é que tras o teorema de Pitágoras demostrouse o teorema inverso: nun triángulo, se o cadrado sobre un lado é a suma de cadrados sobre os outros dous, o ángulo que forman os dous últimos lados é recto.
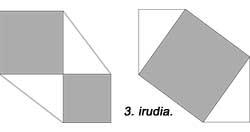
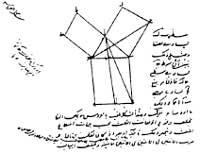
A de Euklides non é a única demostración do teorema. Na figura 2 pódese ver a demostración árabe realizada en 1350. O soado científico renacentista Leonardo dá Vinci ofreceu tamén a súa demostración (Figura 3). No libro “The Pythagean Proposition” de Elisha Scott Loomis (1940) preséntanse 367 demostracións, cada una cunha visión diferente.
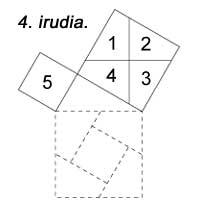
Moitas das probas do teorema utilízanse a miúdo como xogo. Por exemplo, no xogo clásico que aparece na figura 4. Os cadrados dos lados 3 e 4 pódense dividir en 5 pezas e logo formar o lado 5.
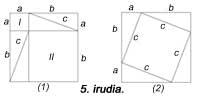
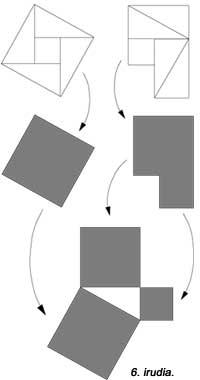
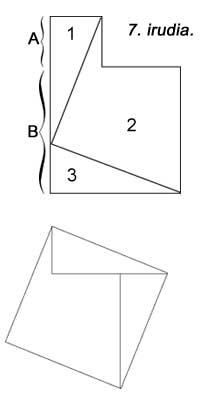
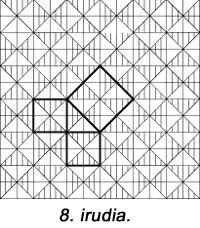
Na seguinte figura aparece outra pero non se utilizaron unidades cadradas. O 6º é similar ao anterior. En todos eles utilízanse cinco pezas. Hilario Fernández Long, ex Reitor da Universidade de Buenos Aires, inventou un puzzle de tres pezas paira demostrar o teorema (figura 7). Aparece outro. E finalmente, na figura 8 demóstrase coa axuda dun mosaico, como facían os babilonios.
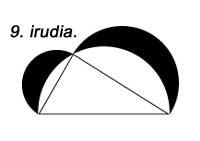
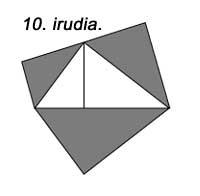
A construción de semicírculos en lugar de cadrados sobre as caras cumpre a mesma propiedade (Figura 9). O mesmo ocorre si construímos triángulos similares (Figura 10).