Essais du théorème de Pythagore
Avec ce nom, on connaît le résultat correspondant à des triangles droits, c'est-à-dire la somme des carrés des catètes est le carré de l'hypotense. Avant Pythagore, il était connu dans d'autres pays comme l'Egypte, Babylone, la Chine, etc. (Les Européens, comme toujours, notre propre gâteau).
Nous savons que Pythagore a voyagé en Egypte et à Babylone, et peut-être en Inde. Dans ces longs voyages, en plus des découvertes religieuses et astronomiques, il a également acquis de nombreuses découvertes mathématiques (Soit dit en passant, Pythagore était contemporain de Bouddha, Confucius et Lao Ts).
Il est généralement reconnu que la science et les mathématiques antérieures à celles de Helena étaient généralement utiles. Cependant, certains indices nous suggèrent qu'il a fait une étude propre des mathématiques. Dans un texte cunéiforme de l'Université de Yale apparaît un carré et ses diagonales. Sur un côté, on peut voir les numéros 30 et 42;25,35 et 1;24,51,10 (les numéros sont représentés dans le système sexagésimal).
Le dernier nombre est le rapport entre la diagonale et les longueurs du côté, et est plus proche de - 2 que le million. Ce niveau de précision est due à la connaissance du théorème de Pythagore. La découverte du théorème de Pythagore ne se limitait pas aux triangles isocèle. Par exemple, dans un ancien problème, on place une échelle de 0;30 de longueur contre un mur et on se demande: combien s'éloignera de la base du mur l'extrémité inférieure de l'escalier, si l'extrémité supérieure descend 0;6 unités?.
Les Babyloniens connaissaient déjà le théorème. Pour justifier le nom a été dit que le théorème de Pythagore a été testé d'abord par les Pythagoriciens, mais cela ne peut pas être vérifié parce qu'il n'y a pas de preuves.
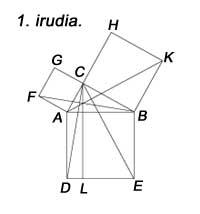
Pas de Pythagore, mais nous connaissons d'autres preuves. Le premier livre d'Euklides se termine par les propositions 47 et 48, dans lequel sont présentés les preuves du théorème de Pythagore et son inverse. Euklides a évité l'utilisation des proportions dans l'exposition en raison des difficultés qui pourraient produire le détournement. Cependant, Euklides, utilisant la figure 1, a effectué une démonstration futée. La démonstration est obtenue: Le carré qui est construit sur le côté AC est le double du triangle FAB ou le double du triangle CAO, qui est égal au rectangle AL. D'autre part, le carré sur le côté BC est le double du triangle ABK ou le double du triangle BCE, c'est-à-dire égal au rectangle BL. Par conséquent, la somme des carrés est égale à la somme des rectangles, c'est-à-dire le carré AB.
Le mérite d'Euklides est qu'après le théorème de Pythagore a été démontré le théorème inverse: dans un triangle, si le carré sur un côté est la somme des carrés sur les deux autres, l'angle qui forment les deux derniers côtés est droite.
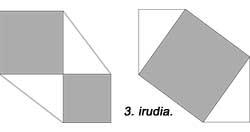
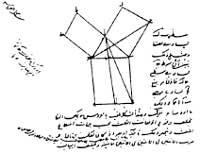
Celle d'Euklides n'est pas la seule démonstration du théorème. La figure 2 montre la démonstration arabe réalisée en 1350. Le célèbre scientifique de la Renaissance Léonard de Vinci offrit aussi sa démonstration (Figure 3). Dans le livre « The Pythagean Proposition » d’Elisha Scott Loomis (1940), 367 démonstrations sont présentées, chacune ayant une vision différente.
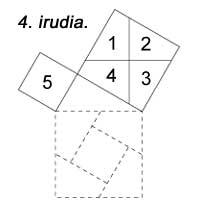
Plusieurs des essais de théorème sont souvent employés comme jeu. Par exemple, dans le jeu classique qui apparaît sur la figure 4. Les carrés des côtés 3 et 4 peuvent être divisés en 5 pièces, puis former le côté 5.
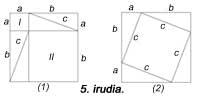
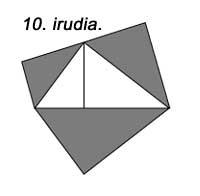
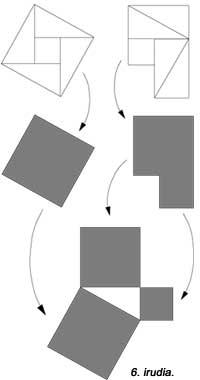
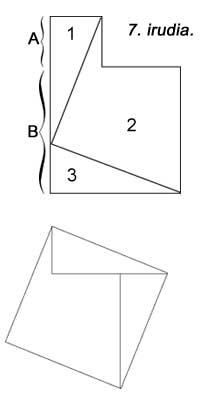
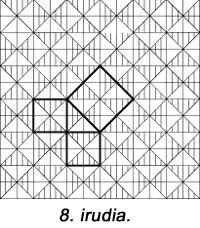
Dans la figure suivante, une autre figure apparaît, mais aucune unité carrée n'a été utilisée. Le 6ème est similaire au précédent. Cinq pièces sont utilisées dans chacun d'eux. Hilario Fernández Long, ancien Recteur de l'Université de Buenos Aires, a inventé un puzzle en trois pièces pour démontrer le théorème (Figure 7). Un autre apparaît. Et enfin, dans la figure 8 est montré avec l'aide d'une mosaïque, comme le faisaient les Babyloniens.
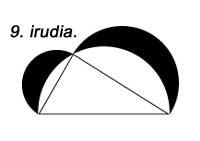
La construction de demi-cercles au lieu de carrés sur les faces remplit la même propriété (figure 9). Il en va de même si nous construisons des triangles similaires (figure 10).