Pruebas del teorema de Pitágoras
Con este nombre se conoce el resultado correspondiente a triángulos rectos, es decir, la suma de cuadrados de los catetos es el cuadrado de la hipotenusa. Antes de Pitágoras era conocido en otros países como Egipto, Babilonia, China, etc. (Los europeos, como siempre, nuestra propia torta).
Sabemos que Pitágoras viajó a Egipto y Babilonia, y quizás a la India. En aquellos largos viajes, además de los descubrimientos religiosos y astronómicos, también adquirió numerosos descubrimientos matemáticos (Por cierto, Pitágoras fue contemporáneo de Buda, Confucio y Lao Ts).
Se suele reconocer que la ciencia y las matemáticas anteriores a las de Helena eran, en general, útiles. Sin embargo, algunos indicios nos sugieren que se hizo un estudio propio de las matemáticas. En un texto cuneiforme de la Universidad de Yale aparece un cuadrado y sus diagonales. Junto a un lado se pueden ver los números 30 y 42;25,35 y 1;24,51,10 (los números están representados en el sistema sexagesimal).
El último número es la relación entre la diagonal y las longitudes del lado, y está más cerca de - 2 que el millón. Este nivel de precisión se debe al conocimiento del teorema de Pitágoras. El descubrimiento del teorema de Pitágoras no se limitaba a los triángulos isósceles. Por ejemplo, en un antiguo problema se coloca una escalera de 0;30 de longitud contra un muro y se pregunta: ¿cuánto se alejará de la base del muro el extremo inferior de la escalera, si el extremo superior baja 0;6 unidades?.
Los babilonios ya conocían el teorema. Para justificar el nombre se ha dicho que el teorema de Pitágoras fue probado primero por los pitagóricos, pero eso no se puede comprobar porque no hay pruebas.
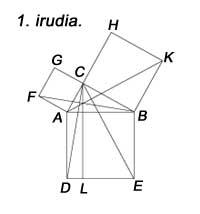
No de Pitágoras, pero conocemos otras pruebas. El primer libro de Euklides concluye con las propuestas 47 y 48, en las que se muestran las pruebas del teorema de Pitágoras y su inversa. Euklides evitó el uso de proporciones en la demostración debido a las dificultades que podía generar la malversación. Sin embargo, Euklides, utilizando la figura 1, realizó una demostración elegante. La demostración se obtiene: El cuadrado que se construye sobre el lado AC es el doble del triángulo FAB o el doble del triángulo CAD, que es igual al rectángulo AL. Por otra parte, el cuadrado sobre el lado BC es el doble del triángulo ABK o el doble del triángulo BCE, es decir, igual al rectángulo BL. En consecuencia, la suma de cuadrados es igual a la suma de rectángulos, es decir, el cuadrado AB.
El mérito de Euklides es que tras el teorema de Pitágoras se ha demostrado el teorema inverso: en un triángulo, si el cuadrado sobre un lado es la suma de cuadrados sobre los otros dos, el ángulo que forman los dos últimos lados es recto.
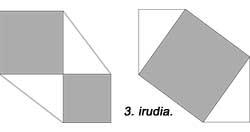
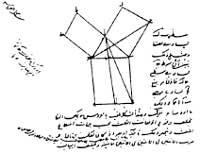
La de Euklides no es la única demostración del teorema. En la figura 2 se puede ver la demostración árabe realizada en 1350. El célebre científico renacentista Leonardo da Vinci ofreció también su demostración (Figura 3). En el libro “The Pythagean Proposition” de Elisha Scott Loomis (1940) se presentan 367 demostraciones, cada una con una visión diferente.
Muchas de las pruebas del teorema se utilizan a menudo como juego. Por ejemplo, en el juego clásico que aparece en la figura 4. Los cuadrados de los lados 3 y 4 se pueden dividir en 5 piezas y luego formar el lado 5.
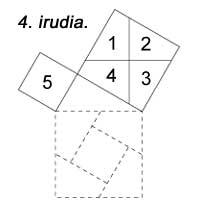
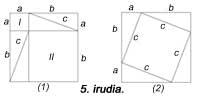
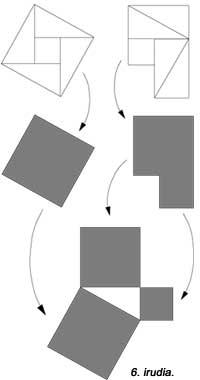
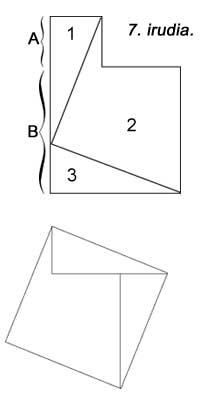
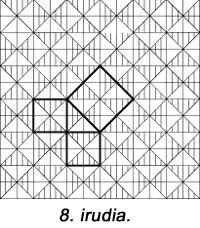
En la siguiente figura aparece otra pero no se han utilizado unidades cuadradas. El 6º es similar al anterior. En todos ellos se utilizan cinco piezas. Hilario Fernández Long, ex Rector de la Universidad de Buenos Aires, inventó un puzzle de tres piezas para demostrar el teorema (figura 7). Aparece otro. Y finalmente, en la figura 8 se demuestra con la ayuda de un mosaico, como hacían los babilonios.
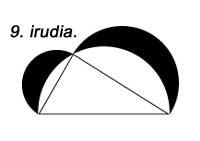
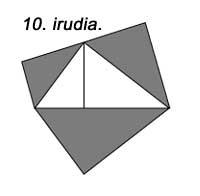
La construcción de semicírculos en lugar de cuadrados sobre las caras cumple la misma propiedad (Figura 9). Lo mismo ocurre si construimos triángulos similares (Figura 10).