Proves del teorema de Pitàgores
Amb aquest nom es coneix el resultat corresponent a triangles rectes, és a dir, la suma de quadrats dels catets és el quadrat de la hipotenusa. Abans de Pitàgores era conegut en altres països com Egipte, Babilònia, la Xina, etc. (Els europeus, com sempre, la nostra pròpia coca).
Sabem que Pitàgores va viatjar a Egipte i Babilònia, i potser a l'Índia. En aquells llargs viatges, a més dels descobriments religiosos i astronòmics, també va adquirir nombrosos descobriments matemàtics (Per cert, Pitàgores va ser contemporani de Buda, Confucio i Lao Ts).
Se sol reconèixer que la ciència i les matemàtiques anteriors a les d'Helena eren, en general, útils. No obstant això, alguns indicis ens suggereixen que es va fer un estudi propi de les matemàtiques. En un text cuneïforme de la Universitat de Yale apareix un quadrat i les seves diagonals. Al costat d'un costat es poden veure els números 30 i 42;25,35 i 1;24,51,10 (els números estan representats en el sistema sexagesimal).
L'últim número és la relació entre la diagonal i les longituds del costat, i està més prop de - 2 que el milió. Aquest nivell de precisió es deu al coneixement del teorema de Pitàgores. El descobriment del teorema de Pitàgores no es limitava als triangles isòsceles. Per exemple, en un antic problema es col·loca una escala de 0;30 de longitud contra un mur i es pregunta: quant s'allunyarà de la base del mur l'extrem inferior de l'escala, si l'extrem superior baixa 0;6 unitats?.
Els babilonis ja coneixien el teorema. Per a justificar el nom s'ha dit que el teorema de Pitàgores va ser provat primer pels pitagòrics, però això no es pot comprovar perquè no hi ha proves.
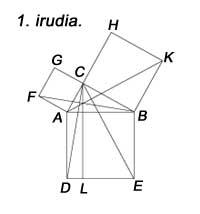
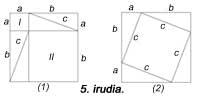
No de Pitàgores, però coneixem altres proves. El primer llibre d'Euklides conclou amb les propostes 47 i 48, en les quals es mostren les proves del teorema de Pitàgores i la seva inversa. Euklides va evitar l'ús de proporcions en la demostració a causa de les dificultats que podia generar la malversació. No obstant això, Euklides, utilitzant la figura 1, va realitzar una demostració elegant. La demostració s'obté: El quadrat que es construeix sobre el costat AC és el doble del triangle FAB o el doble del triangle CAD, que és igual al rectangle AL. D'altra banda, el quadrat sobre el costat BC és el doble del triangle ABK o el doble del triangle BCE, és a dir, igual al rectangle BL. En conseqüència, la suma de quadrats és igual a la suma de rectangles, és a dir, el quadrat AB.
El mèrit d'Euklides és que després del teorema de Pitàgores s'ha demostrat el teorema invers: en un triangle, si el quadrat sobre un costat és la suma de quadrats sobre els altres dos, l'angle que formen els dos últims costats és recte.
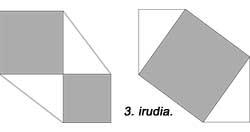
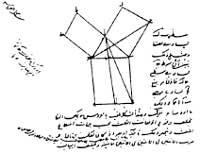
La d'Euklides no és l'única demostració del teorema. En la figura 2 es pot veure la demostració àrab realitzada en 1350. El cèlebre científic renaixentista Leonardo da Vinci va oferir també la seva demostració (Figura 3). En el llibre “The Pythagean Proposition” d'Elisha Scott Loomis (1940) es presenten 367 demostracions, cadascuna amb una visió diferent.
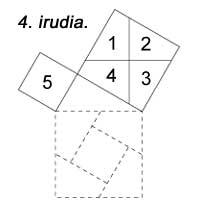
Moltes de les proves del teorema s'utilitzen sovint com a joc. Per exemple, en el joc clàssic que apareix en la figura 4. Els quadrats dels costats 3 i 4 es poden dividir en 5 peces i després formar el costat 5.
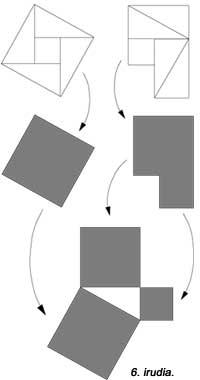
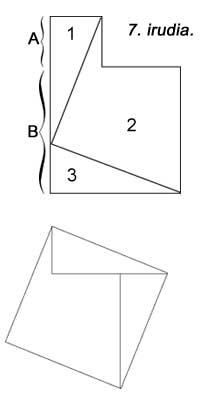
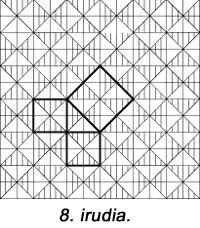
En la següent figura apareix una altra però no s'han utilitzat unitats quadrades. El 6è és similar a l'anterior. En tots ells s'utilitzen cinc peces. Hilario Fernández Long, ex Rector de la Universitat de Buenos Aires, va inventar un puzle de tres peces per a demostrar el teorema (figura 7). Apareix un altre. I finalment, en la figura 8 es demostra amb l'ajuda d'un mosaic, com feien els babilonis.
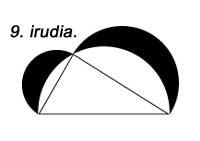
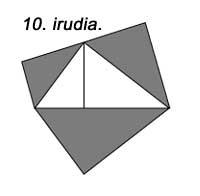
La construcció de semicercles en lloc de quadrats sobre les cares compleix la mateixa propietat (Figura 9). El mateix ocorre si construïm triangles similars (Figura 10).