Pythagorean Theorem Tests
With this name is known the result corresponding to right triangles, that is, the sum of squares of the catetos is the square of the hypotenuse. Before Pythagoras was known in other countries like Egypt, Babylon, China, etc. (Europeans, as always, our own cake).
We know that Pythagoras traveled to Egypt and Babylon, and perhaps to India. In those long journeys, in addition to religious and astronomical discoveries, he also acquired numerous mathematical discoveries (By the way, Pythagoras was contemporary of Buddha, Confucius and Lao Ts).
It is often recognized that science and mathematics prior to Helena's were generally useful. However, some indications suggest that a proper study of mathematics was made. A cuneiform text from Yale University shows a square and its diagonals. Next to one side you can see the numbers 30 and 42;25,35 and 1;24,51,10 (the numbers are represented in the sexagesimal system).
The last number is the relationship between diagonal and side lengths, and is closer to - 2 than the million. This level of precision is due to the knowledge of the Pythagorean theorem. The discovery of the theorem of Pythagoras was not limited to isosceles triangles. For example, in an old problem a ladder of 0;30 in length is placed against a wall and asks: how far away from the base of the wall the lower end of the staircase, if the upper end drops 0;6 units?.
The Babylonians already knew the theorem. To justify the name it has been said that the Pythagorean theorem was first tested by the Pythagoreans, but that cannot be verified because there is no evidence.
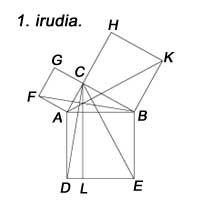
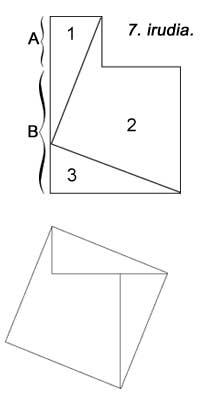
Not from Pythagoras, but we know other tests. The first book of Euklides concludes with proposals 47 and 48, showing the evidence of Pythagorean theorem and its inverse. Euklides avoided the use of proportions in the demonstration due to the difficulties that could generate embezzlement. However, Euklides, using Figure 1, performed an elegant demonstration. The demonstration is obtained: The square that is constructed on the AC side is double the triangle FAB or double the triangle CAD, which is equal to the rectangle AL. On the other hand, the square on the BC side is double the triangle ABK or double the triangle BCE, that is, equal to the rectangle BL. Consequently, the sum of squares is equal to the sum of rectangles, that is, the square AB.
The merit of Euklides is that after the theorem of Pythagoras the reverse theorem has been shown: in a triangle, if the square on one side is the sum of squares on the other two, the angle forming the last two sides is straight.
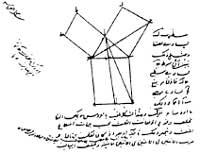
Euklides' is not the only demonstration of the theorem. Figure 2 shows the Arabic demonstration in 1350. The famous Renaissance scientist Leonardo da Vinci also offered his demonstration (Figure 3). In the book “The Pythagean Proposition” by Elisha Scott Loomis (1940) 367 demonstrations are presented, each with a different vision.
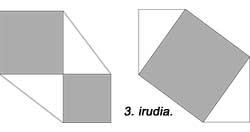
Many of the theorem tests are often used as a game. For example, in the classic game that appears in figure 4. Squares on sides 3 and 4 can be divided into 5 pieces and then form side 5.
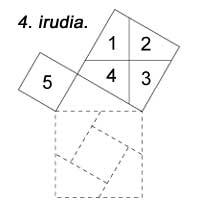
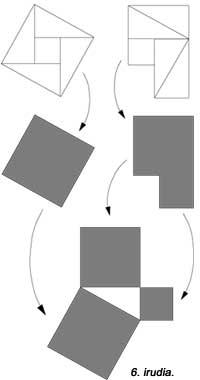
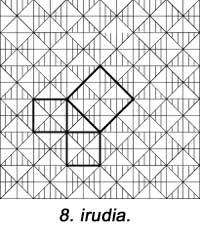
In the following figure appears another but no square units have been used. The 6th is similar to the previous one. All of them use five pieces. Hilario Fernández Long, former Rector of the University of Buenos Aires, invented a three-piece puzzle to demonstrate the theorem (figure 7). Another appears. And finally, figure 8 is shown with the help of a mosaic, as the Babylonians did.
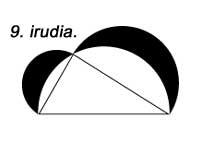
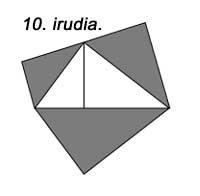
The construction of semicircles instead of squares on the faces fulfills the same property (Figure 9). The same happens if we build similar triangles (Figure 10).