Mathematica (III)
3. Extrémités conditionnées d'une fonction
• Énoncé
Souvent, en calculant les extrémités d'une fonction, on nous donne les conditions qui doivent remplir ces extrêmes. Autrement dit, nous n'aurons qu'à accepter certains résultats. Dans l'exemple suivant, nous allons voir comment les extrémités conditionnées d'une fonction peuvent être calculées via Mathematica.
• Étapes de la résolution
Nous calculerons d'abord les extrémités normales de la fonction, puis nous pourrons les comparer aux extrémités conditionnées. Nous calculerons les extrémités conditionnées en utilisant la méthode de multiplicateurs de Lagrange.
• Commandes à utiliser
D : calcule la dérivée d'une fonction par rapport à la variable donnée.
Solve: c'est l'ordre de résolution des équations.
Union : fait la collecte des listes en supprimant des éléments répétés.
/ : applique la règle ou ensemble de règles qui est indiqué à droite à l'expression gauche.
Plot3D : fait une image tridimensionnelle d'une fonction.
ViewPoint : affiche l'image tridimensionnelle d'un point de vue particulier.
AspecRatio : représente la proportion entre les axes du graphique.
DisplayFunction : permet d'afficher le graphique ou non.
PlotRange : permet de limiter les valeurs de la fonction dans le graphique.
Axes: caractéristique de représenter ou non les axes des graphiques.
Boxed: représente la boîte en images tridimensionnelles.
RGBColor : permet de sélectionner la couleur de l'image d'un graphique.
Point Size : indique la taille du point sur l'image.
Point : adapte les bandes de deux ou trois éléments à un plan ou un point d'espace.
Show: affiche les composants graphiques.
ParametricPlot3D : réalise un graphique tridimensionnel à partir d'équations paramétriques. Il est utilisé pour représenter des surfaces qui ne peuvent pas être exprimées comme fonctions.
Box Ratios : permet d'exprimer les proportions entre les axes des graphiques en trois dimensions.
Contour Plot : représente les courbes de niveau d'une image tridimensionnelle.
ParametricPlot : graphique bidimensionnel à partir d'équations paramétriques. Il est utilisé pour représenter des courbes qui ne peuvent pas être représentées comme des fonctions.
PlotStyle : permet de définir certaines caractéristiques de l'image.
Graphics: convertit les données qui lui sont données en un élément représentable.
Polygon : relie les points attribués par un polygone.
• Résolution par Mathematica
g[x_, y_]:= y3 + x2 et + 2x2 + 2y2 - 4y – 8
Extrémités communes:
d1[x_,y_]:=D[g[x,y],x]d2[x_,y_]:=D[g[x,y],y]
punegon=Solve[{d1[x,y]==0,d2[x,y]==0},{x,y}]punegon=Union[punegon]
{{X B 0, et Règle -2}, {x Règle 0, et Règle -2}, {x B 0, et
B 2},{x B 0, et
B/3}{x B 0, et -2}, {x 0, et B/3}
d11[x_,y_]:=D[g[x,y],{x,2}]d22[x_,y_]:=D[g[x,y],{y,2}]d12[x_,y_]:=D[g[x,y],x,y]
h1[x_,y_]:=d11[x,y]h2[x_,y_]:=d11[x,y]d22[x,y]-d12[x,y]2
hess={1,h1[x,y],h2[x,y]}
hess / punk
{1, 4 + 2 et, -4 x2 + (4 + 2y) (4 + 6y)}{1,
0, 0}, {1, 16/3, 128/3}
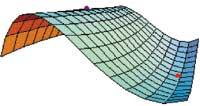
Dans le premier point (0,-2), cette méthode ne nous dit pas ce qui se passe parce qu'il y a des thèmes de la série qui sont zéro. Par conséquent, nous ne pouvons pas décider de la nature de ce point. Au deuxième point (0,2/3), la fonction a un minimum relatif puisque tous les thèmes de la succession des barrières sont positifs.
p0=Plot3D[g[x,y], {x,-1,1}, {y,-3,1}, Point} {1,0.5,0.25}, Ratio False Automatic, DisplayFunction Identity, PlotRange Viewall, Axes False, Bose False]
-Surface Graphics-
mut=Graphics3D[{RGBColor[0.5.0.0.5], Point[0.03], Point[{0,-2.g[0,-2]}], {RGBColor[1.0,0], Point[0.03], Point[{0,2/3.g[0]+0.1}]
-Graphics3D-
Show[p0, mut, DisplayFunction: $DisplayFunction]
-Graphics3D-
Extrêmes conditionnés:
Condition x2+y2=1
F[x_,y_]:=g[x,y]+l(x2+y2-1)
d1F[x_,y_]:=D[x,y],x]d2F[x_,y_]:=D[F[x,y],y]d11F[x_,y_]:=D[x,y],{x,2}]d22F[x_,y,12_]:
pungel=Solve[{d1F[x,y]==0,d2F[x,y]==0,x2+y2==1}, {x,y, l}]
{{l Territoire -(5/2), x Règle 0, et Règle
-1},{l -(3/2), x Règle 0, et Règle 1}
h1F[x_,y_]:=d11F[x,y]h2F[x_,y_]:=d11F[x,y]d22F[x,y]-d12F[x,y]2
hessF={1,h1F[x,y],h2F[x,y]}
{1, 4 + 2y + 2l, -4 x2 + (4 + 2y + 2l) (4 + 6y + 2l)}
hessF / pungel
{{1,-3,21},{1,3,21}
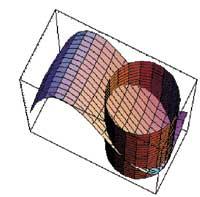
Par conséquent, dans le premier point, (0,-1), a un minimum et dans le second, (0,1), le maximum, selon les signes des thèmes de la succession des clôtures.
zi=ParametricPlot3D[{Cos[t], Sin[t], z}, {t,0,2}, {z,-10,0}, Box Ratios Automatique, DisplayFunction Identity]
-Graphics3D-
p1=Plot3D[g[x,y],{x,-1,1},{y,-3,1}, Box Ratios Règle Automatic, DisplayFunction Règle Identity]
Show[p1, zi, DisplayFunction:?$DisplayFunction,ViewPoint
B {1,0.5,8}]
-Graphics3D-
ps1=Graphics3D[{RGBColor[1,0,0], Point[0.025], Point[{0,1,-9}]}, {RGBColor[0,1], Point[0.025], Point[{0,-1,-3}]]]
-Graphics3D-
mb1=ParametricPlot3D[{Cos[t], Sin[t], -3Sin[t]-6}, {t,0,2{}, ViewPoint
{1,.0.5,8},DisplayFunction Identity]
-Graphics3D-
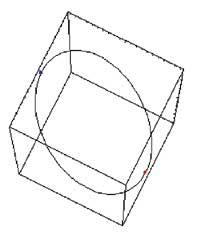
Show[mb1, ps1, DisplayFunction: $DisplayFunction]
-Graphics3D-
kp2=Commune Plot[g[x,y], {x,-2.5,2.5},
{y,-3,1}, SimultanéationRatio automatisé,DisplayFunction Règle
Identity]
-Contour Graphics-
mb2=ParametricPlot[{Cos[t], Sin[t]}, {t,0.2},
PlotStyle RGBCcolor[0,1,0],
Adapté Ratio Établi
Automatique,DisplayFunction Identity]
-Graphics-
ps2=Graphics[{RGBColor[1,0,0], Point[{0.06], Point[{0,1}]}, {RGBColor[0,1], Point Size[0.06], Point[{0,-1}]]
-Graphics-
mut2=Graphics[{RGBColor[0.5.0.5],Polygon[{-0.025,-2.025},{-0.025,-1.975},{0.025,-1.975},{0.025,-2.025},{-0.025,{-0.025},{-0.025,}
-Graphics-
Show[kp2, mb2, mut2, ps2, DisplayFunction:$DisplayFunction]
-Graphics-
• Commentaires
Tout d'abord, nous avons calculé les extrémités normales par la méthode traditionnelle. C'est-à-dire que nous calculons les premières dérivées partielles en utilisant la commande D et nous résolvons le système d'équations qui est généré en égalisant zéro par Solve. La commande Union a été utilisée pour éliminer les solutions répétées du système. Enfin, avec les deuxièmes dérivées partielles, nous avons complété la succession des barrières et déterminé les extrémités en fonction de la succession correspondant à chaque point. Ces extrêmes sont ceux qui peuvent être distingués dans l'image réalisée avec les commandes Plot3D, Graphics3D et Show.
Dans la deuxième partie, la méthode de Lagrange a été utilisée pour calculer les extrémités conditionnées. Pour cela, nous avons utilisé comme avant les commandes D et Solve. Les images tridimensionnelles de fonction et de condition ont ensuite été réalisées en utilisant Plot3D et ParametricPlot3D. Ci-dessous, la courbe d'intersection entre la fonction et la condition et les points trouvés avec les commandes Graphics3D, ParametricPlot3D, Point et Show.
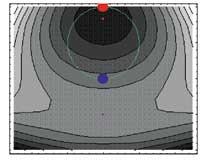
Enfin, une projection supérieure de fonction et de condition (Contour Plot) a été réalisée dans laquelle les extrémités normales (Polygon, carré) ont été placées et conditionnées (Point, cercle).





