Mathematica (III)
3. Extrems condicionats d'una funció
• Enunciat
Moltes vegades, en calcular els extrems d'una funció, ens donen les condicions que han de complir aquests extrems. És a dir, només haurem d'acceptar alguns resultats. En l'exemple següent veurem com es poden calcular els extrems condicionats d'una funció mitjançant Mathematica.
• Passos de la resolució
Primer calcularem els extrems normals de la funció per a després poder comparar-los amb els extrems condicionats. Calcularem els extrems condicionats utilitzant el mètode de multiplicadors de Lagrange.
• Ordres a utilitzar
D: calcula la derivada d'una funció respecte a la variable donada.
Solve: és l'ordre de resolució d'equacions.
Unió: fa la recopilació de llistes eliminant elements repetits.
/ : aplica la regla o conjunt de regles que s'indica a la dreta a l'expressió esquerra.
Plot3D: fa una imatge tridimensional d'una funció.
ViewPoint: mostra la imatge tridimensional des d'un punt de vista concret.
AspecRatio: representa la proporció entre els eixos del gràfic.
DisplayFunction: permet visualitzar el gràfic o no.
PlotRange: permet limitar els valors de la funció en el gràfic.
Axes: característica de representar o no els eixos dels gràfics.
Boxed: representa la caixa en imatges tridimensionals.
RGBColor: serveix per a seleccionar el color de la imatge d'un gràfic.
Point Size: indica la grandària que tindrà el punt en la imatge.
Point: adapta les bandes de dos o tres elements a un pla o punt de l'espai.
Xou: mostra els components gràfics.
ParametricPlot3D: realitza un gràfic tridimensional a partir d'equacions paramètriques. S'utilitza per a representar superfícies que no poden expressar-se com a funcions.
Box Ràtios: permet expressar les proporcions entre els eixos dels gràfics tridimensionals.
Contour Plot: representa les corbes de nivell d'una imatge tridimensional.
ParametricPlot: grafico bidimensional a partir d'equacions paramètriques. S'utilitza per a representar corbes que no es poden representar com a funcions.
PlotStyle: permet definir algunes característiques de la imatge.
Graphics: converteix la dada que se li dóna en un element representable.
Polygon: uneix els punts atorgats mitjançant un polígon.
• Resolució per Mathematica
g[x_, i_]:= y3 + x2 i + 2x2 + 2y2 - 4y – 8
Extrems comuns:
d1[x_,i_]:=D[g[x,i],x]d2[x_,i_]:=D[g[x,i],i]
punegon=Solve[{d1[x,i]==0,d2[x,i]==0},{x,i}]punegon=Union[punegon]
{{X B 0, i Regla -2}, {x Regla 0, i Regla -2}, {x B 0, i
B 2},{x B 0, i
B/3}{{x B 0, i -2}, {x 0, i B/3}}
d11[x_,i_]:=D[g[x,i],{x,2}]d22[x_,i_]:=D[g[x,i],{i,2}]d12[x_,i_]:=D[g[x,i],x,i]
h1[x_,i_]:=d11[x,i]h2[x_,i_]:=d11[x,i]d22[x,i]-d12[x,i]2
hess={1,h1[x,i],h2[x,i]}
hess / punk
{1, 4 + 2 i, -4 x2 + (4 + 2y) (4 + 6y)}{{1,
0, 0}, {1, 16/3, 128/3}
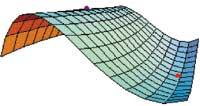
En el primer punt (0,-2), aquest mètode no ens diu el que passa perquè hi ha temes de la sèrie que són zero. Per tant, no podem decidir la naturalesa d'aquest punt. En el segon punt (0,2/3), en canvi, la funció té un mínim relatiu ja que tots els temes de la successió de barreres són positius.
p0=Plot3D[g[x,i], {x,-1,1}, {i,-3,1}, ViewPoint} {1,0.5,0.25}, AspectRatio False Automatic, DisplayFunction Identity, PlotRange> All, Axes False, Bose False]
-Surface Graphics-
mut=Graphics3D[{{RGBColor[0.5.0.0.5], Point[0.03], Point[{0,-2.g[0,-2]}], {RGBColor[1.0,0], Point[0.03], Point[{0,2/3.g[0]+0.1}]
-Graphics3D-
Xou[p0, mut, DisplayFunction:>$DisplayFunction]
-Graphics3D-
Extrems condicionats:
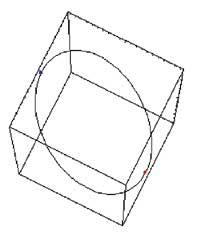
Condició x2+y2=1
F[x_,i_]:=g[x,i]+l(x2+y2-1)
d1F[x_,i_]:=D[x,i],x]d2F[x_,i_]:=D[F[x,i],i]d11F[x_,i_]:=D[F[x,i],{x,2}]d22F[x_,i,12_]:
pungel=Solve[{d1F[x,i]==0,d2F[x,i]==0,x2+y2==1}, {x,i, l}]
{{l Territori -(5/2), x Regla 0, i Regla
-1},{l -(3/2), x Regla 0, i Regla 1}
h1F[x_,i_]:=d11F[x,i]h2F[x_,i_]:=d11F[x,i]d22F[x,i]-d12F[x,i]2
hessF={1,h1F[x,i],h2F[x,i]}
{1, 4 + 2y + 2l, -4 x2 + (4 + 2y + 2l) (4 + 6y + 2l)}
hessF / pungel
{{1,-3,21},{1,3,21}
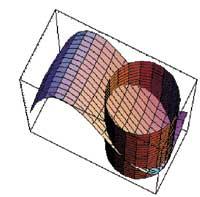
Per tant, en el primer punt, (0,-1), té un mínim i en el segon, (0,1), el màxim, segons els signes dels temes de la successió de tanques.
zi=ParametricPlot3D[{Cos[t], Sense[t], z}, {t,0,2>}, {z,-10,0}, Box Ràtios Regla Automatic, DisplayFunction Identity]
-Graphics3D-
p1=Plot3D[g[x,i],{x,-1,1},{i,-3,1}, Box Ràtios Regla Automatic, DisplayFunction Regla Identity]
Xou[p1, zi, DisplayFunction:>$DisplayFunction,ViewPoint
B {1,0.5,8}]
-Graphics3D-
ps1=Graphics3D[{{RGBColor[1,0,0], Point[0.025], Point[{0,1,-9}]}, {RGBColor[0,0,1], Point[0.025], Point[{0,-1,-3}]]
-Graphics3D-
mb1=ParametricPlot3D[{Cos[t], Sense[t], -3Sin[t]-6}, {t,0,2{}, ViewPoint
{1,.0.5,8},DisplayFunction> Identity]
-Graphics3D-
Xou[mb1, ps1, DisplayFunction:>$DisplayFunction]
-Graphics3D-
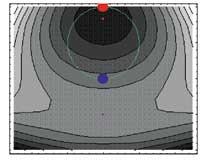
kp2=ConcanalPlot[g[x,i], {x,-2.5,2.5}, {i,-3,1},
AspectRatio> Automatic,DisplayFunction Regla
Identity]
-Contour Graphics-
mb2=ParametricPlot[{Cos[t], Sense[t]}, {t,0.2},
PlotStyle> RGBCcolor[0,1,0],
AspectRatio Establert
Automatic,DisplayFunction Identity]
-Graphics-
ps2=Graphics[{{RGBColor[1,0,0], Point[{0.06], Point[{0,1}]}, {RGBColor[0,0,1], Point Size[0.06], Point[{0,-1}]]
-Graphics-
mut2=Graphics[{{RGBColor[0.5.0.5],Polygon[{-0.025,-2.025},{-0.025,-1.975},{0.025,-1.975},{0.025,-2.025},{-0.025,{-0.025},{-0.025,}
-Graphics-
Xou[kp2, mb2, mut2, ps2, DisplayFunction:>$DisplayFunction]
-Graphics-
• Comentaris
En primer lloc, hem calculat els extrems normals mitjançant el mètode tradicional. És a dir, calculem les primeres derivades parcials utilitzant l'ordre D i resolem el sistema d'equacions que es genera igualant amb zero a través de Solve. S'ha utilitzat l'ordre Unió per a eliminar les solucions repetides del sistema. Finalment, amb les segones derivades parcials hem completat la successió de barreres i hem determinat els extrems en funció de la successió corresponent a cada punt. Aquests extrems són els que es poden distingir en la imatge realitzada amb les ordres Plot3D, Graphics3D i Xou.
En la segona part s'ha utilitzat el mètode de Lagrange per a calcular els extrems condicionats. Per a això ens hem valgut com abans de les ordres D i Solve. A continuació s'han realitzat les imatges tridimensionals de funció i condició utilitzant Plot3D i ParametricPlot3D. Més a baix s'ha representat la corba d'intersecció entre funció i condició i els punts oposats amb les ordres Graphics3D, ParametricPlot3D, Point i Xou.
Finalment, s'ha realitzat una projecció superior de funció i condició (Contour Plot) en la qual s'han col·locat els extrems normals (Polygon, quadrat) i condicionats (Point, cercle).





