Mathematica (III)
3. Extremos condicionados de una función
• Enunciado
Muchas veces, al calcular los extremos de una función, nos dan las condiciones que deben cumplir esos extremos. Es decir, sólo tendremos que aceptar algunos resultados. En el ejemplo siguiente veremos cómo se pueden calcular los extremos condicionados de una función mediante Mathematica.
• Pasos de la resolución
Primero calcularemos los extremos normales de la función para luego poder compararlos con los extremos condicionados. Calcularemos los extremos condicionados utilizando el método de multiplicadores de Lagrange.
• Órdenes a utilizar
D: calcula la derivada de una función respecto a la variable dada.
Solve: es la orden de resolución de ecuaciones.
Unión: hace la recopilación de listas eliminando elementos repetidos.
/ : aplica la regla o conjunto de reglas que se indica a la derecha a la expresión izquierda.
Plot3D: hace una imagen tridimensional de una función.
ViewPoint: muestra la imagen tridimensional desde un punto de vista concreto.
AspecRatio: representa la proporción entre los ejes del gráfico.
DisplayFunction: permite visualizar el gráfico o no.
PlotRange: permite limitar los valores de la función en el gráfico.
Axes: característica de representar o no los ejes de los gráficos.
Boxed: representa la caja en imágenes tridimensionales.
RGBColor: sirve para seleccionar el color de la imagen de un gráfico.
Point Size: indica el tamaño que tendrá el punto en la imagen.
Point: adapta las bandas de dos o tres elementos a un plano o punto del espacio.
Show: muestra los componentes gráficos.
ParametricPlot3D: realiza un gráfico tridimensional a partir de ecuaciones paramétricas. Se utiliza para representar superficies que no pueden expresarse como funciones.
Box Ratios: permite expresar las proporciones entre los ejes de los gráficos tridimensionales.
Contour Plot: representa las curvas de nivel de una imagen tridimensional.
ParametricPlot: grafico bidimensional a partir de ecuaciones paramétricas. Se utiliza para representar curvas que no se pueden representar como funciones.
PlotStyle: permite definir algunas características de la imagen.
Graphics: convierte el dato que se le da en un elemento representable.
Polygon: une los puntos otorgados mediante un polígono.
• Resolución por Mathematica
g[x_, y_]:= y3 + x2 y + 2x2 + 2y2 - 4y – 8
Extremos comunes:
d1[x_,y_]:=D[g[x,y],x]d2[x_,y_]:=D[g[x,y],y]
punegon=Solve[{d1[x,y]==0,d2[x,y]==0},{x,y}]punegon=Union[punegon]
{{X B 0, y Regla -2}, {x Regla 0, y Regla -2}, {x B 0, y
B 2},{x B 0, y
B/3}{{x B 0, y -2}, {x 0, y B/3}}
d11[x_,y_]:=D[g[x,y],{x,2}]d22[x_,y_]:=D[g[x,y],{y,2}]d12[x_,y_]:=D[g[x,y],x,y]
h1[x_,y_]:=d11[x,y]h2[x_,y_]:=d11[x,y]d22[x,y]-d12[x,y]2
hess={1,h1[x,y],h2[x,y]}
hess / punk
{1, 4 + 2 y, -4 x2 + (4 + 2y) (4 + 6y)}{{1,
0, 0}, {1, 16/3, 128/3}
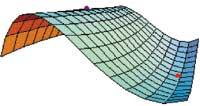
En el primer punto (0,-2), este método no nos dice lo que pasa porque hay temas de la serie que son cero. Por lo tanto, no podemos decidir la naturaleza de este punto. En el segundo punto (0,2/3), en cambio, la función tiene un mínimo relativo ya que todos los temas de la sucesión de barreras son positivos.
p0=Plot3D[g[x,y], {x,-1,1}, {y,-3,1}, ViewPoint} {1,0.5,0.25}, AspectRatio False Automatic, DisplayFunction Identity, PlotRange> All, Axes False, Bose False]
-Surface Graphics-
mut=Graphics3D[{{RGBColor[0.5.0.0.5], Point[0.03], Point[{0,-2.g[0,-2]}], {RGBColor[1.0,0], Point[0.03], Point[{0,2/3.g[0]+0.1}]
-Graphics3D-
Show[p0, mut, DisplayFunction:>$DisplayFunction]
-Graphics3D-
Extremos condicionados:
Condición x2+y2=1
F[x_,y_]:=g[x,y]+l(x2+y2-1)
d1F[x_,y_]:=D[x,y],x]d2F[x_,y_]:=D[F[x,y],y]d11F[x_,y_]:=D[F[x,y],{x,2}]d22F[x_,y,12_]:
pungel=Solve[{d1F[x,y]==0,d2F[x,y]==0,x2+y2==1}, {x,y, l}]
{{l Territorio -(5/2), x Regla 0, y Regla
-1},{l -(3/2), x Regla 0, y Regla 1}
h1F[x_,y_]:=d11F[x,y]h2F[x_,y_]:=d11F[x,y]d22F[x,y]-d12F[x,y]2
hessF={1,h1F[x,y],h2F[x,y]}
{1, 4 + 2y + 2l, -4 x2 + (4 + 2y + 2l) (4 + 6y + 2l)}
hessF / pungel
{{1,-3,21},{1,3,21}
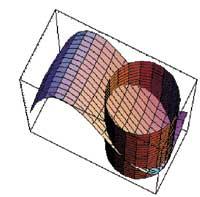
Por tanto, en el primer punto, (0,-1), tiene un mínimo y en el segundo, (0,1), el máximo, según los signos de los temas de la sucesión de vallas.
zi=ParametricPlot3D[{Cos[t], Sin[t], z}, {t,0,2>}, {z,-10,0}, Box Ratios Regla Automatic, DisplayFunction Identity]
-Graphics3D-
p1=Plot3D[g[x,y],{x,-1,1},{y,-3,1}, Box Ratios Regla Automatic, DisplayFunction Regla Identity]
Show[p1, zi, DisplayFunction:>$DisplayFunction,ViewPoint
B {1,0.5,8}]
-Graphics3D-
ps1=Graphics3D[{{RGBColor[1,0,0], Point[0.025], Point[{0,1,-9}]}, {RGBColor[0,0,1], Point[0.025], Point[{0,-1,-3}]]
-Graphics3D-
mb1=ParametricPlot3D[{Cos[t], Sin[t], -3Sin[t]-6}, {t,0,2{}, ViewPoint
{1,.0.5,8},DisplayFunction> Identity]
-Graphics3D-
Show[mb1, ps1, DisplayFunction:>$DisplayFunction]
-Graphics3D-
kp2=ConcanalPlot[g[x,y], {x,-2.5,2.5}, {y,-3,1},
AspectRatio> Automatic,DisplayFunction Regla
Identity]
-Contour Graphics-
mb2=ParametricPlot[{Cos[t], Sin[t]}, {t,0.2},
PlotStyle> RGBCcolor[0,1,0],
AspectRatio Establecido
Automatic,DisplayFunction Identity]
-Graphics-
ps2=Graphics[{{RGBColor[1,0,0], Point[{0.06], Point[{0,1}]}, {RGBColor[0,0,1], Point Size[0.06], Point[{0,-1}]]
-Graphics-
mut2=Graphics[{{RGBColor[0.5.0.5],Polygon[{-0.025,-2.025},{-0.025,-1.975},{0.025,-1.975},{0.025,-2.025},{-0.025,{-0.025},{-0.025,}
-Graphics-
Show[kp2, mb2, mut2, ps2, DisplayFunction:>$DisplayFunction]
-Graphics-
• Comentarios
En primer lugar, hemos calculado los extremos normales mediante el método tradicional. Es decir, calculamos las primeras derivadas parciales utilizando la orden D y resolvemos el sistema de ecuaciones que se genera igualando con cero a través de Solve. Se ha utilizado la orden Unión para eliminar las soluciones repetidas del sistema. Por último, con las segundas derivadas parciales hemos completado la sucesión de barreras y hemos determinado los extremos en función de la sucesión correspondiente a cada punto. Estos extremos son los que se pueden distinguir en la imagen realizada con las órdenes Plot3D, Graphics3D y Show.
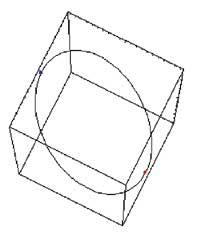
En la segunda parte se ha utilizado el método de Lagrange para calcular los extremos condicionados. Para ello nos hemos valido como antes de las órdenes D y Solve. A continuación se han realizado las imágenes tridimensionales de función y condición utilizando Plot3D y ParametricPlot3D. Más abajo se ha representado la curva de intersección entre función y condición y los puntos encontrados con las órdenes Graphics3D, ParametricPlot3D, Point y Show.
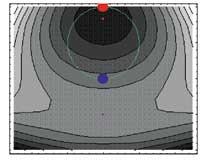
Por último, se ha realizado una proyección superior de función y condición (Contour Plot) en la que se han colocado los extremos normales (Polygon, cuadrado) y condicionados (Point, círculo).





