Mathematica (et IV)

Cet article conclut l'exemple suivant que nous avons organisé comme introduction au programme Mathematica. Bien que nous ayons limité les exercices au domaine du calcul mathématique, rappelez-vous que Mathematica est un outil approprié pour utiliser des matrices, résoudre des systèmes d'équations, etc. Dans la confiance qu'ils lui seraient de valeur, voici le dernier exemple.

4º Volume délimité par les deux surfaces

  • Énoncé

Nous calculons maintenant le volume qui délimite les deux surfaces dans l'espace. Pour cela, nous utiliserons une double intégrale. Pour définir les limites des intégrales, nous représenterons les projections de surfaces de différents points de vue.

  • Étapes de la résolution

Nous calculerons d'abord les extrémités normales de la fonction, puis nous pourrons les comparer aux extrémités conditionnées. Nous calculerons les extrémités conditionnées en utilisant la méthode de multiplicateurs de Lagrange.

  • Instructions à utiliser
  1. ParametricPlot3D : réalise un graphique tridimensionnel à partir d'équations paramétriques. Il est utilisé pour représenter des surfaces qui ne peuvent pas être exprimées comme fonctions.
  2. ViewPoint : affiche l'image tridimensionnelle d'un point de vue particulier.
  3. DisplayFunction : permet d'afficher le graphique ou de le garder caché.
  4. Show: affiche les composants graphiques.
  5. Graphics: convertira les données qui lui sont données en un élément représentable.
  6. Circle: avec centre et rayon représente la circonférence.
  7. Disk: avec centre et rayon représente le cercle.
  8. Rectangle: représente le rectangle avec les sommets inférieur gauche et supérieur droit.
  9. RGBCouleur: couleur de l'image d'un graphique.
  10. Axes: caractéristique de représenter ou non les axes des graphiques.
  11. AspecRatio: caractéristique de représenter la proportion entre les axes du graphique.
  12. ViewPoint : affiche l'image tridimensionnelle d'un point de vue particulier.
  13. Intégrate: calcule l'intégrale. En utilisant deux variables, il calcule l'intégrale double.
  14. Simplify : simplifie une expression algébrique.
    %, fait référence au résultat précédent.
  • Résolution par Mathematica

Équations cartésiennes:

cadran x2 + y2 + z2 = Cylindre 4: x2 + y2 - 2y = 0

Équations paramétriques:

sphère:

x = 2cos[t] cos[v],

cylindre:

 x = 2sin[t] cos[t],
et = 2sin[t] cos[v], et = 2sen[t]2,
z = 2sen[v], z = z

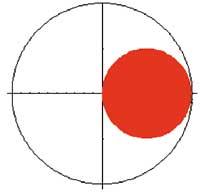
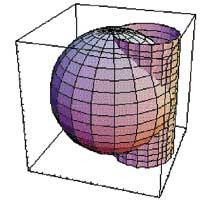
Image tridimensionnelle:

e = ParametricPlot3D[{2cos[t][v], 2sin[t]cos[v], 2sin[v]}, {t,0,2ler}, {v,-/2,ler/2}, View{3,1,1.5}, DisplayFunction Identity]

-Graphics3D-

z = ParametricPlot3D[ {2sin[t]cos[t],2sin[t]2,z}, {t,0,2{}, {z,-2,2}, ViewPoint Règle {3,1,1.5}, DisplayFunction

-Graphics3D-

Show[e, z, DisplayFunction: $DisplayFunction]

-Graphics3D-

Projection en plan:

pc=Graphics[{Circle[{0,0},2], {RGBColor[1,0,0], Disk[{1,0},1]}, Axe True, Ratio Automatic]

-Graphics3D-

Show[xliff-newline]

-Graphics3D-

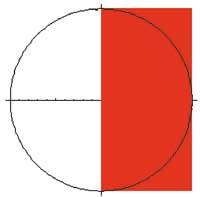
Projection préalable:

Abr=Graphics[{RGolor[1,0,0], Rectangle[{0,-2},{2,2}]}, Circle[{0,0},2]}, Axes- True,{ Ratio-Automatic]

-Graphics3D-

Show[avr]

-Graphics3D-

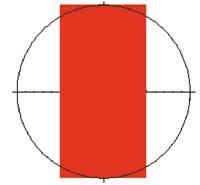
Projection de la droite:

epr=Graphics[{{RGBColor[1,0,0], Rectangle[{-1,-2},{1,2}]}, Circle[{0,0},2]}, Axes True, Ratio Règle Automatique]

-Graphics3D-

Show[epr, Axes True]

-Graphics3D-

Double intégral:

Limites des intégrales en coordonnées cartésiennes:

et prudencio [0, 2],x Convient [-] (2 et - y2), » (2 et - y2)]intégré: z = » (4 - x2 - y2).

Limites des intégrales en coordonnées cylindriques:

t Prudencio [0,_],r Espace[0, 2sen[t],

intégrant

z = r * (4 - r2)

Remarque : avec ces limites, nous ne calculerons que la moitié supérieure du volume.

Integrate[r*Sqrt[4-r2],{t,0,{},{r,0,2sin[t]}]?8/3
+ 4/9 (-4 + 3ess) - 4/9 (4 + 3?)
Simplify[%]
8/9 (-4 + 3ler)

C'est la moitié supérieure du volume. Par conséquent, le volume total:

2 * 16/9
(-4 + 3ash)

  • Commentaires

Nous avons d'abord fait une image en trois dimensions pour capturer l'idée de volume. Pour ce faire, nous avons utilisé les commandes traditionnelles ParametricPlot3D et Show et avons choisi l'approche standard via la fonctionnalité ViewPoint. Ensuite, nous avons représenté les trois projections de volume, supérieure, avant et droite, en utilisant les commandes Disk, Rectangle, Circle, Graphics et Show. Nous y avons également utilisé DisplayFunction, RGBColor, Ratio et Axes. Enfin, nous avons calculé le double intégral avec la commande Integrate et simplifié le résultat par Simplify. De cette façon, nous avons obtenu la moitié du volume. Le volume total est obtenu en multipliant le résultat précédent (%) par deux.

Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila