Mathematica (y IV)

Con este artículo damos por finalizado el siguiente ejemplo que hemos organizado como introducción al programa Mathematica. Aunque hemos limitado los ejercicios al campo del cálculo matemático, recordad que Mathematica es una herramienta adecuada para utilizar matrices, resolver sistemas de ecuaciones, etc. En la confianza de que le serían de valor, a continuación se muestra el último ejemplo.

4º Volumen delimitado por las dos superficies

  • Enunciado

Calculamos ahora el volumen que delimitan ambas superficies en el espacio. Para ello utilizaremos una doble integral. Para definir los límites de las integrales, representaremos las proyecciones de superficies desde diferentes puntos de vista.

  • Pasos de la resolución

Primero calcularemos los extremos normales de la función para luego poder compararlos con los extremos condicionados. Calcularemos los extremos condicionados utilizando el método de multiplicadores de Lagrange.

  • Instrucciones a utilizar
  1. ParametricPlot3D: realiza un gráfico tridimensional a partir de ecuaciones paramétricas. Se utiliza para representar superficies que no pueden expresarse como funciones.
  2. ViewPoint: muestra la imagen tridimensional desde un punto de vista concreto.
  3. DisplayFunction: permite visualizar el gráfico o mantenerlo oculto.
  4. Show: mostrará los componentes gráficos.
  5. Graphics: convertirá el dato que se le da en un elemento representable.
  6. Circle: con centro y radio representa la circunferencia.
  7. Disk: con centro y radio representa el círculo.
  8. Rectangle: representa el rectángulo con los vértices inferior izquierdo y superior derecho.
  9. RGBColor: color de la imagen de un gráfico.
  10. Axes: característica de representar o no los ejes de los gráficos.
  11. AspecRatio: característica de representar la proporción entre los ejes del gráfico.
  12. ViewPoint: muestra la imagen tridimensional desde un punto de vista concreto.
  13. Integrate: calcula la integral. Mediante dos variables, calcula la integral doble.
  14. Simplify: simplifica una expresión algebraica.
    %, hace referencia al resultado anterior.
  • Resolución por Mathematica

Ecuaciones cartesianas:

esfera x2 + y2 + z2 = Cilindro 4: x2 + y2 - 2y = 0

Ecuaciones paramétricas:

esfera:

x = 2cos[t] cos[v],

cilindro:

 x = 2sin[t] cos[t],
y = 2sin[t] cos[v], y = 2sen[t]2,
z = 2sen[v], z = z

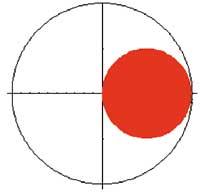
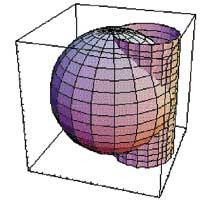
Imagen tridimensional:

e = ParametricPlot3D[{2cos[t]cos[v], 2sin[t]cos[v], 2sin[v]}, {t,0,2ler}, {v,-cer/2,ler/2}, View>{3,1,1.5}, DisplayFunction <Identity]

-Graphics3D-

z = ParametricPlot3D[ {2sin[t]cos[t],2sin[t]2,z}, {t,0,2{}, {z,-2,2}, ViewPoint Regla {3,1,1.5}, DisplayFunction> Identity]

-Graphics3D-

Show[e, z, DisplayFunction: $DisplayFunction]

-Graphics3D-

Proyección en planta:

pc=Graphics[{Circle[{0,0},2], {RGBColor[1,0,0], Disk[{1,0},1]}, Axes> True, AspectRatio Automatic]

-Graphics3D-

Show[xliff-newline]

-Graphics3D-

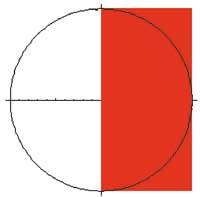
Proyección previa:

Abr=Graphics[{{RGBColor[1,0,0], Rectangle[{0,-2},{2,2}]}, Circle[{0,0},2]}, Axes- True, AspectRatio-Automatic]

-Graphics3D-

Show[abr]

-Graphics3D-

Proyección desde la derecha:

epr=Graphics[{{RGBColor[1,0,0], Rectangle[{-1,-2},{1,2}]}, Circle[{0,0},2]}, Axes> True, AspectRatio Regla Automatic]

-Graphics3D-

Show[epr, Axes> True]

-Graphics3D-

Integral doble:

Límites de integrales en coordenadas cartesianas:

y Prudencio [0, 2],x Conviene [-] (2 y - y2), » (2 y - y2)]integrado: z = » (4 - x2 - y2).

Límites de integrales en coordenadas cilíndricas:

t Prudencio [0,_],r Espacio[0, 2sen[t],

integrando

z = r * (4 - r2)

Nota: con estos límites sólo calcularemos la mitad superior del volumen.

Integrate[r*Sqrt[4-r2],{t,0,{},{r,0,2sin[t]}]?8/3
+ 4/9 (-4 + 3ess) - 4/9 (4 + 3?)
Simplify[%]
8/9 (-4 + 3ler)

Esto es la mitad superior del volumen. Por tanto, el volumen total:

2 * 16/9
(-4 + 3ash)

  • Comentarios

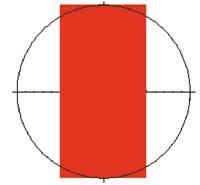
Primero hemos hecho una imagen tridimensional para captar la idea de volumen. Para ello hemos utilizado las tradicionales órdenes ParametricPlot3D y Show y hemos elegido el enfoque estándar a través de la característica ViewPoint. A continuación, hemos representado las tres proyecciones de volumen, la superior, la frontal y la derecha, utilizando las órdenes Disk, Rectangle, Circle, Graphics y Show. En ella también hemos aprovechado DisplayFunction, RGBColor, AspectRatio y Axes. Por último, hemos calculado la integral doble con la orden Integrate y simplificamos el resultado mediante Simplify. De esta forma hemos conseguido la mitad del volumen. El volumen total se obtiene multiplicando el resultado anterior (%) por dos.

Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila