Catro ou cinco colorees
Cantas cores necesítanse paira pintar un mapa para que dúas rexións contiguas sexan de distintas cores?
Facer mapas de catro colorees non é moi difícil. Pódese demostrar que é suficiente con cinco colorees paira todos os mapas. Pero, é suficiente e necesario utilizar catro colorees?, é dicir, poderíase facer un mapa de cinco colorees?

A pesar de que se indicou que os primeiros en utilizar catro colorees eran cartógrafos, parece que o primeiro en explicar a conxectura foi o alumno de Francis Guthrie Edinburgh. El comentouno ao seu irmán, o químico Frederick, quen o fixo saber ao seu profesor de matemáticas Augustus Morgan en 1852. A conxectura fíxose famosa cando o gran matemático Arthur Cayley recoñeceu que en 1878 o tema fora inútil. Enseguida expuxéronse numerosas probas do teorema. Pronto se darían conta de que todos tiñan algún erro.
N. Wiener, creador da cibermática, admitiu que na autobiografía “Ex-Prodigy” atopouse co problema (como todos os matemáticos) e que fracasou. A situación actual do problema (que sabemos) é a seguinte: Comprobouse que se cumpre en todos os mapas que non teñen máis de 38 comarcas. O resultado é escaso. Con todo, tendo en conta que hai máis de 1038 mapas diferentes, parece que non é tan malo. Os computadores actuais tampouco poderían analizar todas as configuracións no tempo adecuado.
Si o problema é atractivo e fascinante é porque parece fácil de demostrar. A ausencia de probas na actualidade é irritante, tendo en conta que teoremas similares demostráronse paira superficies máis complexas. Por exemplo, en superficies unilaterais, a cinta de Möbius, a botella de Klein e o plano proyectivo, demostrouse que o número de cores suficiente e necesario é 6. En Torua esta cifra é de 7. (A esfera é equivalente neste problema ao plano).
Paira comprender a dificultade do problema exporémosche un xogo. Poden participar dous ou máis xogadores. O obxectivo é atopar un mapa que requira cinco colorees.
O primeiro xogador representará una rexión.
O segundo pintará a rexión anterior e representará outra
O seguinte pintará a última rexión e representará a outra (con límite cunha das rexións anteriores).
Hai que seguir así ata que un xogador necesite a quinta cor.
Paira seguir profundando no problema, velaquí outro tres exercicios.
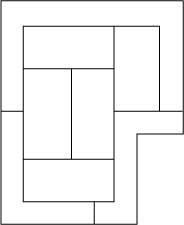
Cantas cores necesítanse paira pintar a figura 1 para que as dúas rexións cun límite común non teñan o mesmo cor?
Supoñamos que se quere pintar a figura 2 con 4 cores. Trátase de pintar cada rexión dunha cor e dúas zonas contiguas de diferente cor. A zona superior ten una superficie de 16 dm2 e o resto de 8 dm2. A pintura está tan vermella como paira encher 24 dm2, a amarela está tan vermella como a vermella, a verde 16 dm2 e a azul está lenta paira cumprir 8 dm2. Como facelo?
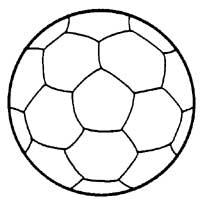
No balón de fútbol hai 32 rexións: 20 hexagonales e 12 pentagonales. Cantas cores necesítanse paira pintar as 32 comarcas, paira evitar que dúas rexións do mesma cor teñan límites comúns? Catro debe ser suficiente. Proba no balón e non na imaxe.
Una vez realizados os “exercicios” anteriores, creemos que serás capaz de comprender a esencia do problema. Desgraciadamente é difícil demostrar que cinco colorees son suficientes paira calquera mapa chairo. Con todo, a demostración do teorema a dúas cores pódese incluír neste artigo.
Consideremos todos os mapas planos que se poden construír utilizando liñas rectas (como o damero). 4a. si tómase o mapa da imaxe non será difícil demostrar que só se necesitan dúas cores paira pintar. Si engadimos una recta a calquera mapa formado por rectas (recta negra da imaxe), a nova recta divide o mapa en dous partes. Cada un polo seu lado estaría ben pintado, pero a ambos os dous lados da recta hai rexións do mesma cor. Paira conseguir una situación óptima bastaría con intercambiar cores no mapa dun lado da recta (4b. Imaxe).
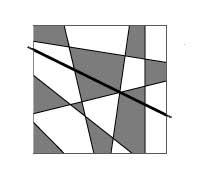
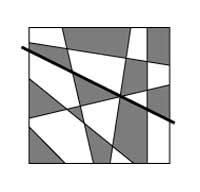
Si debuxamos outra recta, deberiamos facer o mesmo, é dicir, intercambiaremos as cores do mapa ao carón da recta. O razoamento pódese aplicar a calquera número de rectas e así, mediante a indución matemática, demóstrase que son dúas cores suficientes paira pintar todos os mapas que se poden obter directamente.

A demostración pode estenderse a mapas formados por liñas abertas e indefinidas e curvas pechadas sen espiral (Figura 5). Si engádese una liña que atravesa o mapa, as cores das rexións situadas ao carón deben cambiar. Si a curva é pechada, cambiarán as cores das rexións interiores (ou exteriores). Tamén se poden introducir curvas espirales, pero dificúltase o procedemento de recalentamiento.
Hai que ter en conta que neste tipo de mapas todos os vértices son pares, é dicir, crúzanse dúas liñas. Pódese demostrar que a condición suficiente e necesaria paira poder pintar un mapa con dúas cores é que todos os vértices sexan pares.
Por último, e a modo de exercicio, colle un mapa sen pintar e tenta pintar co menor número de cores posible.





