Four or five colors
How many colors are needed to paint a map so that two contiguous regions are of different colors?
Making maps of four colors is not very difficult. It can be shown that it is enough with five colors for all maps. But is it enough and necessary to use four colors? That is, could you make a five-color map?

Although it has been indicated that the first to use four colors were cartographers, it seems that the first to explain the conjecture was the student of Francis Guthrie Edinburgh. He commented it to his brother, the chemist Frederick, who let him know to his mathematics teacher Augustus Morgan in 1852. The conjecture became famous when the great mathematician Arthur Cayley recognized that in 1878 the subject had been useless. Numerous proofs of the theorem were then presented. They would soon realize that everyone had some mistake.
N. Wiener, creator of the cybermatic, admitted that in the autobiography “Ex-Prodigy” he encountered the problem (like all mathematicians) and failed. The current situation of the problem (which we know) is as follows: It has been proven to be true on all maps with no more than 38 regions. The result is scarce. However, considering that there are more than 1038 different maps, it seems not so bad. Current computers also could not analyze all settings at the right time.
If the problem is attractive and fascinating it is because it seems easy to demonstrate. The absence of evidence today is irritating, given that similar theorems have been shown for more complex surfaces. For example, on unilateral surfaces, Möbius tape, Klein bottle and projective plane, it has been shown that the number of colors sufficient and necessary is 6. In Torua this figure is 7. (The sphere is equivalent in this problem to the plane.)
To understand the difficulty of the problem we will present a game. Two or more players can participate. The goal is to find a map that requires five colors.
The first player will represent a region.
The second will paint the previous region and represent another
The next will paint the last region and represent another (bordering one of the previous regions).
You have to follow this until a player needs the fifth color.
To continue deepening the problem, here are three other exercises.
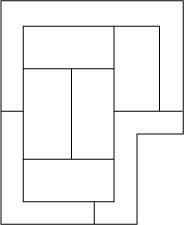
How many colors are needed to paint Figure 1 so that the two regions with a common boundary do not have the same color?
Suppose you want to paint figure 2 with 4 colors. It is about painting each region of a color and two contiguous areas of different color. The upper area has an area of 16 dm2 and the rest of 8 dm2. The paint is as red as to fill 24 dm2, the yellow is as red as the red, the green 16 dm2 and the blue is slow to meet 8 dm2. How to do it?
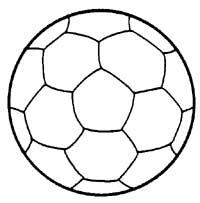
In football there are 32 regions: 20 hexagonal and 12 pentagonal. How many colors are needed to paint the 32 regions, to prevent two regions of the same color from having common limits? Four must be enough. Try the ball and not the image.
Once the previous “exercises” are done, we believe you will be able to understand the essence of the problem. Unfortunately it is difficult to prove that five colors are sufficient for any plain map. However, the two-color theorem demonstration can be included in this article.
Consider all flat maps that can be built using straight lines (like the damero). 4th. if you take the picture map it will not be difficult to prove that only two colors are needed to paint. If we add a line to any map formed by straight lines (black line of the image), the new line divides the map into two parts. Each on its side would be well painted, but on both sides of the line there are regions of the same color. To achieve an optimal situation it would be enough to exchange colors on the map on one side of the straight (4b. Image).
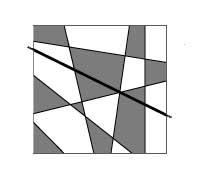
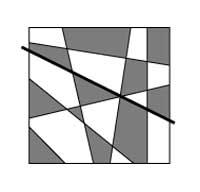
If we draw another straight line, we should do the same, that is, we will exchange the colors of the map to one side of the straight line. Reasoning can be applied to any number of lines and thus, by mathematical induction, it is shown that they are two enough colors to paint all maps that can be obtained directly.

The demonstration can be extended to maps formed by open and indefinite lines and closed curves without spiral (Figure 5). If you add a line that crosses the map, the colors of the regions next to you must change. If the curve is closed, the colors of the interior (or exterior) regions will change. Spiral curves may also be inserted, but the reheating procedure is difficult.
Note that in this type of maps all vertices are even, that is, two lines cross. It can be demonstrated that the sufficient and necessary condition to be able to paint a map with two colors is that all vertices are even.
Finally, as an exercise, take an unpainted map and try to paint with as few colors as possible.





