Cuatro o cinco colores
¿Cuántos colores se necesitan para pintar un mapa para que dos regiones contiguas sean de distintos colores?
Hacer mapas de cuatro colores no es muy difícil. Se puede demostrar que es suficiente con cinco colores para todos los mapas. Pero, ¿es suficiente y necesario utilizar cuatro colores?, es decir, ¿se podría hacer un mapa de cinco colores?

A pesar de que se ha indicado que los primeros en utilizar cuatro colores eran cartógrafos, parece que el primero en explicar la conjetura fue el alumno de Francis Guthrie Edinburgh. Él lo comentó a su hermano, el químico Frederick, quien lo hizo saber a su profesor de matemáticas Augustus Morgan en 1852. La conjetura se hizo famosa cuando el gran matemático Arthur Cayley reconoció que en 1878 el tema había sido inútil. Enseguida se expusieron numerosas pruebas del teorema. Pronto se darían cuenta de que todos tenían algún error.
N. Wiener, creador de la cibermática, admitió que en la autobiografía “Ex-Prodigy” se encontró con el problema (como todos los matemáticos) y que fracasó. La situación actual del problema (que sabemos) es la siguiente: Se ha comprobado que se cumple en todos los mapas que no tienen más de 38 comarcas. El resultado es escaso. Sin embargo, teniendo en cuenta que hay más de 1038 mapas diferentes, parece que no es tan malo. Los ordenadores actuales tampoco podrían analizar todas las configuraciones en el tiempo adecuado.
Si el problema es atractivo y fascinante es porque parece fácil de demostrar. La ausencia de pruebas en la actualidad es irritante, teniendo en cuenta que teoremas similares se han demostrado para superficies más complejas. Por ejemplo, en superficies unilaterales, la cinta de Möbius, la botella de Klein y el plano proyectivo, se ha demostrado que el número de colores suficiente y necesario es 6. En Torua esta cifra es de 7. (La esfera es equivalente en este problema al plano).
Para comprender la dificultad del problema te plantearemos un juego. Pueden participar dos o más jugadores. El objetivo es encontrar un mapa que requiera cinco colores.
El primer jugador representará una región.
El segundo pintará la región anterior y representará otra
El siguiente pintará la última región y representará a otra (con límite con una de las regiones anteriores).
Hay que seguir así hasta que un jugador necesite el quinto color.
Para seguir profundizando en el problema, he aquí otros tres ejercicios.
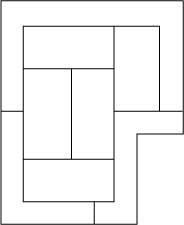
¿Cuántos colores se necesitan para pintar la figura 1 para que las dos regiones con un límite común no tengan el mismo color?
Supongamos que se quiere pintar la figura 2 con 4 colores. Se trata de pintar cada región de un color y dos zonas contiguas de diferente color. La zona superior tiene una superficie de 16 dm2 y el resto de 8 dm2. La pintura está tan roja como para llenar 24 dm2, la amarilla está tan roja como la roja, la verde 16 dm2 y la azul está lenta para cumplir 8 dm2. ¿Cómo hacerlo?
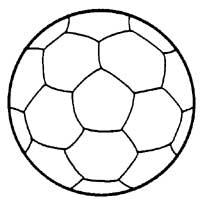
En el balón de fútbol hay 32 regiones: 20 hexagonales y 12 pentagonales. ¿Cuántos colores se necesitan para pintar las 32 comarcas, para evitar que dos regiones del mismo color tengan límites comunes? Cuatro debe ser suficiente. Prueba en el balón y no en la imagen.
Una vez realizados los “ejercicios” anteriores, creemos que serás capaz de comprender la esencia del problema. Desgraciadamente es difícil demostrar que cinco colores son suficientes para cualquier mapa llano. Sin embargo, la demostración del teorema a dos colores se puede incluir en este artículo.
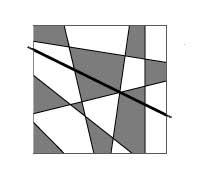
Consideremos todos los mapas planos que se pueden construir utilizando líneas rectas (como el damero). 4a. si se toma el mapa de la imagen no será difícil demostrar que sólo se necesitan dos colores para pintar. Si añadimos una recta a cualquier mapa formado por rectas (recta negra de la imagen), la nueva recta divide el mapa en dos partes. Cada uno por su lado estaría bien pintado, pero a ambos lados de la recta hay regiones del mismo color. Para conseguir una situación óptima bastaría con intercambiar colores en el mapa de un lado de la recta (4b. Imagen).
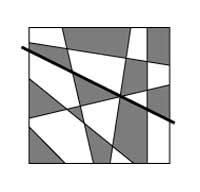
Si dibujamos otra recta, deberíamos hacer lo mismo, es decir, intercambiaremos los colores del mapa a un lado de la recta. El razonamiento se puede aplicar a cualquier número de rectas y así, mediante la inducción matemática, se demuestra que son dos colores suficientes para pintar todos los mapas que se pueden obtener directamente.

La demostración puede extenderse a mapas formados por líneas abiertas e indefinidas y curvas cerradas sin espiral (Figura 5). Si se añade una línea que atraviesa el mapa, los colores de las regiones situadas a un lado deben cambiar. Si la curva es cerrada, cambiarán los colores de las regiones interiores (o exteriores). También se pueden introducir curvas espirales, pero se dificulta el procedimiento de recalentamiento.
Hay que tener en cuenta que en este tipo de mapas todos los vértices son pares, es decir, se cruzan dos líneas. Se puede demostrar que la condición suficiente y necesaria para poder pintar un mapa con dos colores es que todos los vértices sean pares.
Por último, y a modo de ejercicio, coge un mapa sin pintar e intenta pintar con el menor número de colores posible.





