Quatre o cinc colors
Quants colors es necessiten per a pintar un mapa perquè dues regions contigües siguin de diferents colors?
Fer mapes de quatre colors no és molt difícil. Es pot demostrar que és suficient amb cinc colors per a tots els mapes. Però, és suficient i necessari utilitzar quatre colors?, és a dir, es podria fer un mapa de cinc colors?

A pesar que s'ha indicat que els primers a utilitzar quatre colors eren cartògrafs, sembla que el primer a explicar la conjectura va ser l'alumne de Francis Guthrie Edinburgh. Ell ho va comentar al seu germà, el químic Frederick, qui ho va fer saber al seu professor de matemàtiques Augustus Morgan en 1852. La conjectura es va fer famosa quan el gran matemàtic Arthur Cayley va reconèixer que en 1878 el tema havia estat inútil. De seguida es van exposar nombroses proves del teorema. Aviat s'adonarien que tots tenien algun error.
N. Wiener, creador de la cibermática, va admetre que en l'autobiografia “Ex-Prodigy” es va trobar amb el problema (com tots els matemàtics) i que va fracassar. La situació actual del problema (que sabem) és la següent: S'ha comprovat que es compleix en tots els mapes que no tenen més de 38 comarques. El resultat és escàs. No obstant això, tenint en compte que hi ha més de 1038 mapes diferents, sembla que no és tan dolent. Els ordinadors actuals tampoc podrien analitzar totes les configuracions en el temps adequat.
Si el problema és atractiu i fascinant és perquè sembla fàcil de demostrar. L'absència de proves en l'actualitat és irritant, tenint en compte que teoremes similars s'han demostrat per a superfícies més complexes. Per exemple, en superfícies unilaterals, la cinta de Möbius, l'ampolla de Klein i el pla projectiu, s'ha demostrat que el nombre de colors suficient i necessari és 6. En Torua aquesta xifra és de 7. (L'esfera és equivalent en aquest problema al pla).
Per a comprendre la dificultat del problema et plantejarem un joc. Poden participar dos o més jugadors. L'objectiu és trobar un mapa que requereixi cinc colors.
El primer jugador representarà una regió.
El segon pintarà la regió anterior i representarà una altra
El següent pintarà l'última regió i representarà a una altra (amb límit amb una de les regions anteriors).
Cal seguir així fins que un jugador necessiti el cinquè color.
Per a continuar aprofundint en el problema, heus aquí altres tres exercicis.
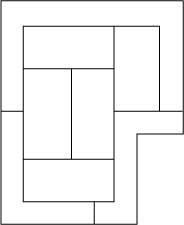
Quants colors es necessiten per a pintar la figura 1 perquè les dues regions amb un límit comú no tinguin el mateix color?
Suposem que es vol pintar la figura 2 amb 4 colors. Es tracta de pintar cada regió d'un color i dues zones contigües de diferent color. La zona superior té una superfície de 16 dm2 i la resta de 8 dm2. La pintura està tan vermella com per a omplir 24 dm2, la groga està tan vermella com la vermella, la verda 16 dm2 i la blava està lenta per a complir 8 dm2. Com fer-ho?
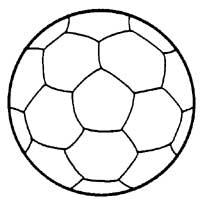
En la pilota de futbol hi ha 32 regions: 20 hexagonals i 12 pentagonals. Quants colors es necessiten per a pintar les 32 comarques, per a evitar que dues regions del mateix color tinguin límits comuns? Quatre ha de ser suficient. Prova en la pilota i no en la imatge.
Una vegada realitzats els “exercicis” anteriors, creiem que seràs capaç de comprendre l'essència del problema. Desgraciadament és difícil demostrar que cinc colors són suficients per a qualsevol mapa pla. No obstant això, la demostració del teorema a dos colors es pot incloure en aquest article.
Considerem tots els mapes plans que es poden construir utilitzant línies rectes (com l'escaquer). 4a. si es pren el mapa de la imatge no serà difícil demostrar que només es necessiten dos colors per a pintar. Si afegim una recta a qualsevol mapa format per rectes (recta negra de la imatge), la nova recta divideix el mapa en dues parts. Cadascun pel seu costat estaria ben pintat, però a banda i banda de la recta hi ha regions del mateix color. Per a aconseguir una situació òptima bastaria amb intercanviar colors en el mapa d'un costat de la recta (4b. Imatge).
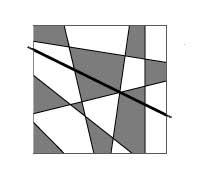
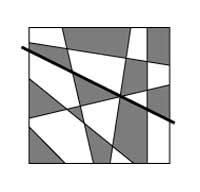
Si dibuixem una altra recta, hauríem de fer el mateix, és a dir, intercanviarem els colors del mapa a un costat de la recta. El raonament es pot aplicar a qualsevol nombre de rectes i així, mitjançant la inducció matemàtica, es demostra que són dos colors suficients per a pintar tots els mapes que es poden obtenir directament.

La demostració pot estendre's a mapes formats per línies obertes i indefinides i corbes tancades sense espiral (Figura 5). Si s'afegeix una línia que travessa el mapa, els colors de les regions situades a un costat han de canviar. Si la corba és tancada, canviaran els colors de les regions interiors (o exteriors). També es poden introduir corbes espirals, però es dificulta el procediment de reescalfament.
Cal tenir en compte que en aquesta mena de mapes tots els vèrtexs són parells, és a dir, es travessen dues línies. Es pot demostrar que la condició suficient i necessària per a poder pintar un mapa amb dos colors és que tots els vèrtexs siguin paris.
Finalment, i a manera d'exercici, agafa un mapa sense pintar i intenta pintar amb el menor nombre de colors possible.





