Lauzpabost kolore

Zabaldu:
Twitter
Facebook
Emaila

Zenbat kolore behar da mapa bat pintatzeko, elkarren ondoko bi eskualde kolore desberdinekoak izan daitezen?

Lau kolore behar dituzten mapak egitea ez da oso zaila. Mapa guztietarako bost kolorerekin nahikoa dela froga daiteke. Baina, lau kolore erabiltzea nahikoa eta beharrezkoa ote da?, hau da, bost kolore behar dituen mapa egin al liteke?

1. irudia.

Lau kolore erabiltzea nahikoa eta beharrezkoa zela esandako lehenengoak kartografoak izan zirela adierazi bada ere, badirudi aierua azaldu zuen lehenengoa Francis Guthrie Edinburgh-eko ikaslea izan zela. Hark bere anaia Frederick kimikariari aipatu zion eta beronek 1852an bere matematika-irakasle zen Augustus Morgan-i jakin erazi zion. Aierua famatu bihurtu zen Arthur Cayley matematikari handiak 1878an gaia aztertzen alferrik ihardun zuela onartu zuenean. Berehala teoremaren frogapen ugari azaldu zen. Laster konturatuko ziren, ordea, guztiek hutsen bat zutela.

N. Wiener-ek, zibermatikaren sortzaileak, “Ex-Prodigy” izeneko autobiografian problemarekin topo egin zuela (matematikari guztiek bezala) eta porrot egin zuela onartu zuen. Problemaren egungo egoera (guk dakigula) hauxe da: 38 eskualde baino gehiago ez dituzten mapa guztietan betetzen dela frogatu da. Emaitza eskasa dela pentsa liteke. Hala ere, 1038 mapa desberdin baino gehiago dagoela kontutan hartuz, badirudi ez dela hain kaskarra. Oraingo ordenadoreek ere ezingo lituzkete denbora egokian konfigurazio guztiak aztertu.

Problema erakargarria eta liluragarria bada, frogatzen erraza dirudielako da. Gaur egun frogapenik gabe egotea sumingarria da, antzeko teoremak gainazal konplexuagoetarako frogatu direla kontutan hartuz. Esate baterako, alde bakarreko gainazaletan, Möbius-en xingola, Klein-en botila eta plano proiektiboan, kolore-kopuru nahikoa eta beharrezkoa 6 dela frogatu da. Toruan, aldiz, 7 da kopuru hori. (Esfera, problema honi dagokionez, planoaren baliokidea da).

2. irudia.

Problemaren zailtasunaz jabetzeko, joko bat planteatuko dizugu. Bik, edo jokalari gehiagok, har dezakete parte. Helburua, bost kolore behar dituen mapa aurkitzea da.

Lehenengo jokalariak eskualde bat irudikatuko du.

Bigarrenak aurreko eskualdea pintatu eta beste bat irudikatuko du

bi eskualdeek muga amankomuna behar dute izan

Hurrengoak azkeneko eskualdea pintatu eta beste bat irudikatuko du (aurreko eskualdeetako batekin muga duelarik).

Horrela segitu behar da, jokalari batek bostgarren kolorearen beharra izan arte.

Probleman sakontzen segitzeko, hona hemen beste hiru ariketa.

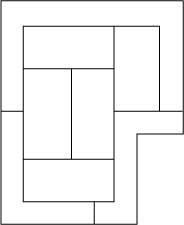
Zenbat kolore behar dira 1. irudia pintatzeko, muga amankomuna duten bi eskualdek kolore bera izan ez dezaten?

Demagun 2. irudia 4 kolorerekin pintatu nahi dela. Eskualde bakoitza kolore batez eta ondoz ondoko bi eskualde kolore desberdinez pintatu nahi dira. Goiko eskualdeak 16 dm²-ko azalera eta gainerakoek 8 dm²-koa dute. 24 dm² betetzeko adina pintura gorria dago; horia ere gorria bezainbeste dago; berdea 16 dm² eta urdina 8 dm² betetzeko lain dago. Nola egin behar da?

3. irudia.

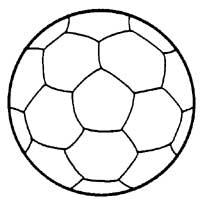
Futbol-baloian 32 eskualde daude: 20 hexagonalak eta 12 pentagonalak. Zenbat kolore behar da 32 eskualdeak pintatzeko, kolore bereko bi eskualdek muga amankomunik izan ez dezaten?. Lauk nahikoa izan behar du. Saia zaitez baloian bertan eta ez irudian.

3. irudia

Aurreko “ariketak” egin eta gero, problemaren mamia ulertzeko gai izango zarelakoan gaude. Edozein mapa launetarako bost kolore nahikoa dela frogatzea, tamalez, zaila da. Baina, bi koloretarako teoremaren frogapena honelako artikuluan sartzeko modukoa da.

Kontsidera ditzagun lerro zuzenak erabiliz eraiki daitezkeen mapa laun guztiak (dama-taula, esaterako). 4a. irudiko mapa hartuz gero ez da zaila izango pintatzeko bi kolore baino ez dela behar frogatzea. Zuzenez osatutako edozein mapari beste zuzen bat eransten badiogu (irudiko zuzen beltza), zuzen berriak mapa bi zatitan banatuko du. Bakoitza, bere aldetik hartuz, ondo pintatuta legoke, baina zuzenaren bi aldeetan kolore bereko eskualdeak daude. Egoera egokia lortzeko, zuzenaren alde bateko mapan koloreak trukatzea nahikoa litzateke (4b. irudia).

4a. eta 4b. irudiak.

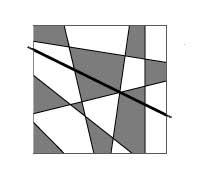
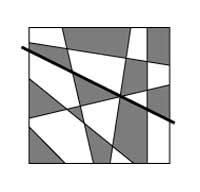
Beste zuzen bat marraztuz gero, gauza bera egin beharko genuke, hau da, zuzenaren alde bateko maparen koloreak trukatu egin beharko ditugu. Arrazonamendua edozein zuzen-kopururi aplika dakioke, eta horrela, indukzio matematikoaren bidez, zuzenen bidez lor daitezkeen mapa guztiak pintatzeko bi kolore nahikoa direla frogatzen da.

5. irudia.

Frogapena zabal daiteke lerro ireki eta mugagabeez eta kiribilik gabeko kurba itxiez osatutako mapetara (5. irudia). Mapa zeharkatzen duen lerro bat eransten bada, alde batera dauden eskualdeen koloreak aldatu egin behar dira. Kurba itxia bada, barruko (edo kanpoko) eskualdeen koloreak aldatu egingo dira. Kurba kiribilak ere sar daitezke, baina berriz kolorea emateko prozedura zaildu egiten da.

Kontutan hartu behar da horrelako mapetan erpin guztiak bikoitiak direla, hots, bi lerro gurutzatzen direla. Mapa bat bi kolorerekin pintatu ahal izateko baldintza nahikoa eta beharrezkoa erpin guztiak bikoitiak izatea dela froga daiteke.

Azkenik, eta ariketa-modura, hartzazu pintatu gabe dagoen maparen bat eta saia zaitez ahal den kolore gutxien erabiliz mapa pintatzen.