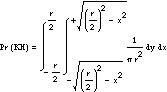Paradoxo de Kord
En xeral podemos dicir que o paradoxo é un razoamento que nos contradi, que pode ser real, falso ou non un nin outro. Os paradoxos sempre existiron. Por exemplo, no tempo dos filósofos gregos Akhilleo e a tartaruga, o cretano Epimenides, etc., sempre houbo quebradizos de cabeza paira filósofos e matemáticos. Pero XIX. Foi a finais do século XX cando este problema alcanzou o seu máximo esplendor. Naquela época, debido a uns paradoxos incomprensibles, as bases das matemáticas cambaleáronse e toda a casa estivo a piques de caer. Aínda que se conseguiu explicar a maioría dos paradoxos, existen actualmente paradoxos sen resolver. Outras tiveron moitas interpretacións.
O paradoxo que propomos hoxe non é delas, como se explicará ao final do artigo, pero creemos que é una curiosidade. Este paradoxo sitúase no campo das Estatísticas, concretamente no cálculo de probabilidades.
Empecemos por expor o problema, a dicir mellor a pregunta: trazamos una circunferencia. Tamén o triángulo equilátero inscrito na circunferencia. A pregunta é: si trazamos una corda, cal é a probabilidade de que a lonxitude da mesma sexa maior que a parte do triángulo?
A continuación preséntanse tres soluciones diferentes que responden a esta pregunta.
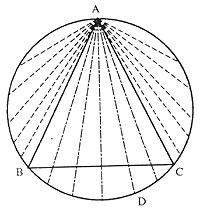
Marcamos a circunferencia e o triángulo equilátero. Sexa o punto A un vértice do triángulo. Consideraranse as cordas trazadas desde o punto A. Como se pode apreciar na figura, para que a zona da corda sexa máis longa que a zona, debemos colocala dentro do ángulo correspondente ao vértice A. E neste caso, si os outros vértices do triángulo son B e C, o outro extremo da corda (D) debe estar no arco da circunferencia entre os puntos B e C.
Se movemos o punto A por a circunferencia, teriamos o mesmo resultado. A lonxitude da circunferencia é 2 r e a do arco BC 2 r/3. Definindo a probabilidade como o cociente entre os casos favorables e os posibles, os casos ao noso favor son 2 r/3 e os casos posibles 2 r. Por tanto, probabilidade
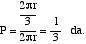
Paira responder á mesma pregunta, esta vez actuaremos doutra maneira. Neste caso tomaremos un lado do triángulo e trazaremos as cordas paralelas a ese lado. Observando o diámetro perpendicular a estas cordas, obsérvase que as cordas máis longas que o lado do triángulo ocupan medio diámetro. Tendo en conta todo isto, obtense que os casos posibles son 2r e os casos favorables r. Por tanto, neste caso a probabilidade
Se se move o triángulo obtense o mesmo resultado.
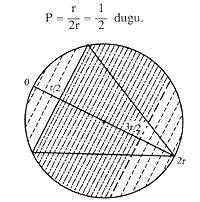
Isto non é suficiente e vexamos a terceira resposta. Tomemos agora os puntos centrais dos lados do triángulo. Se facemos virar o triángulo con respecto ao centro da circunferencia, estes puntos centrais dos lados describirán outra circunferencia. Para que as cordas sexan máis longas que as caras, os puntos centrais das cordas deben estar dentro do círculo que delimita esta última circunferencia.
Neste caso non fixamos nin o triángulo nin ningún punto. Por tanto, calcularemos directamente a probabilidade, sendo os casos favorables (r/2) 2 e os posibles r 2.
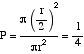
Paira responder ao mesmo problema obtivemos tres resultados diferentes. Como se explica este paradoxo?
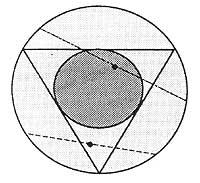
Non debemos quedarnos na pel. Se analizamos as tres condutas, na primeira tomamos a lonxitude da circunferencia paira calcular a probabilidade. No segundo a lonxitude do diámetro e no terceiro a superficie do círculo. É dicir, nos tres casos baseamos a probabilidade en diferentes espazos de probabilidade. Por tanto, os resultados obtidos non son comparables.
Este problema é un exemplo do paradoxo de Beltran.
Leamos a seguinte frase:
Os matemáticos obteñen diferentes números ao calcular a probabilidade de certos sucesos. De feito, os diferentes modelos matemáticos lévannos a resultados diferentes, e o desacordo entre eles é a causa da discrepancia entre resultados.
A análise máis exhaustiva dos diferentes modelos estatísticos preséntase no cadro adxunto, cunha instrumentación matemática máis útil.
Vexamos, pois, os modelos estatísticos correspondentes a tres formulacións diferentes. Na notación que imos utilizar será un feito que sexa maior que a diferenza KH = Corda.
Paira fixar a corda na primeira vista basta con seleccionar un punto da circunferencia, o outro vértice é o punto A. Por tanto, sendo esta elección totalmente aleatoria ou aleatoria e comprendida entre [0,2 r], o modelo estatístico correspondente é una distribución uniforme. Así, paira calcular a probabilidade do suceso KH, os valores que poden tomar as variables aleatorias deben estar no intervalo [2 r/3, 3 r/3]. Por tanto:
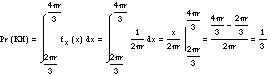
Na segunda formulación, é dicir, cando trazamos paralelos ao carón, cumprirase o suceso KH só se seleccionamos un punto no intervalo [r/2, 3r/2] no diámetro asociado aos paralelos. A esta elección correspóndelle outra variable aleatoria uniforme, pero agora no intervalo [0.2r]. A probabilidade do suceso GC calcúlase como:
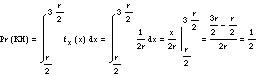
No último punto de vista será maior que o lado da corda raiada, só se o punto medio da corda está dentro do círculo pequeno. Dado que este punto está no plano, terá dúas coordenadas (x,e) e si situamos os eixos de coordenadas no centro do círculo, o suceso GC x 2 +e 2 (r/2) cumprirase cando a ecuación 2 sexa certa. Hai que ter en conta que neste caso (X,E) trátase dunha variable aleatoria bidimensional cuxo campo é un gran círculo. É dicir, a súa función de densidade
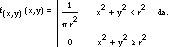
Tendo en conta todo isto, podemos calcular a probabilidade do suceso GC da seguinte maneira: