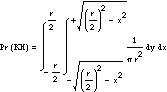Kord Paradox
In general we can say that the paradox is a reasoning that contradicts us, that can be real, false or not one or the other. Paradoxes have always existed. For example, in the time of the Greek philosophers Akhilleo and the turtle, the cretan Epimenides, etc., there have always been headaches for philosophers and mathematicians. But XIX. It was at the end of the 20th century when this problem reached its peak. At that time, due to incomprehensible paradoxes, the foundations of mathematics staggered and the whole house was about to fall. While most paradoxes have been explained, there are currently unresolved paradoxes. Others have had many interpretations.
The paradox that we propose today is not of them, as will be explained at the end of the article, but we believe it is a curiosity. This paradox is situated in the field of statistics, specifically in the calculation of probabilities.
Let's start by posing the problem, to say better the question: we draw a circle. Also the equilateral triangle inscribed in the circumference. The question is: if we draw a string, what is the probability that the length of it is greater than the part of the triangle?
Below are three different solutions that answer this question.
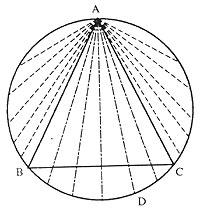
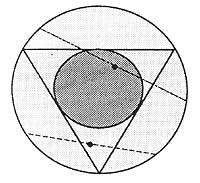
We mark the circumference and the equilateral triangle. Be the point A to a vertex of the triangle. The strings drawn from point A will be considered. As can be seen in the figure, to make the rope area longer than the area, we must place it within the angle corresponding to the vertex A. And in this case, if the other vertices of the triangle are B and C, the other end of the string (D) should be in the arc of the circumference between points B and C.
If we move point A by circumference, we would have the same result. The circumference length is 2 r and the arc length BC 2 r/3. Defining probability as the quotient between favorable and possible cases, the cases in our favor are 2 r/3 and the possible cases 2 r. Therefore, probability
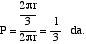
To answer the same question, this time we will act differently. In this case we will take one side of the triangle and draw the parallel strings to that side. Observing the diameter perpendicular to these strings, it is observed that the strings longer than the side of the triangle occupy half diameter. Considering all this, you get that the possible cases are 2nd and favorable cases r. Therefore, in this case the probability
If you move the triangle you get the same result.
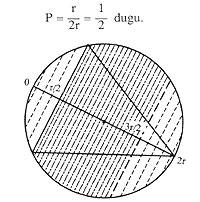
This is not enough and let's see the third answer. Let us now take the center points of the sides of the triangle. If we spin the triangle with respect to the center of the circumference, these central points on the sides will describe another circumference. For the strings to be longer than the faces, the central points of the strings must be within the circle that delimits this last circumference.
In this case we have not fixed neither the triangle nor any point. Therefore, we will directly calculate the probability, being the favorable cases (r/2) 2 and the possible r 2.
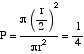
To answer the same problem we have obtained three different results. How is this paradox explained?
We should not stay on the skin. If we analyze the three behaviors, in the first we have taken the circumference length to calculate the probability. In the second diameter length and in the third circle surface. That is, in all three cases we have based probability on different probability spaces. Therefore, the results obtained are not comparable.
This problem is an example of Beltran's paradox.
Read the following sentence:
Mathematicians obtain different numbers by calculating the probability of certain events. In fact, the different mathematical models lead us to different results, and disagreement between them is the cause of the discrepancy between results.
The most comprehensive analysis of the different statistical models is presented in the attached table, with more useful mathematical instrumentation.
Let's look at the statistical models corresponding to three different approaches. In the notation we will use it will be a fact that is greater than the difference KH = Corda.
To fix the rope in the first sight just select one point of the circumference, the other vertex is point A. Therefore, being this choice totally random or random and between [0.2 r], the corresponding statistical model is a uniform distribution. Thus, to calculate the probability of the KH event, the values that random variables can take must be in the interval [2 r/3, 3 r/3]. Therefore:
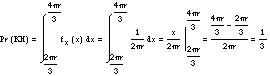
In the second approach, that is, when we draw parallels to one side, the KH event will be fulfilled only if we select a point in the interval [r/2, 3r/2] in the diameter associated with the parallels. This choice corresponds to another uniform random variable, but now in the interval [0.2r]. The probability of the GC event is calculated as:
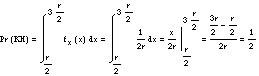
At the last point of view it will be greater than the side of the striped rope, only if the midpoint of the rope is within the small circle. Since this point is in the plane, it will have two coordinates (x,y) and if we place the coordinate axes in the center of the circle, the event GC x 2 +y 2 (r/2) will be fulfilled when equation 2 is true. Bear in mind that in this case (X,Y) it is a two-dimensional random variable whose field is a large circle. That is, its density function
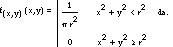
Taking all this into account, we can calculate the probability of the GC event as follows: