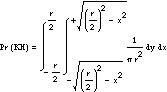Paradoja de Kord
En general podemos decir que la paradoja es un razonamiento que nos contradice, que puede ser real, falso o no uno ni otro. Las paradojas siempre han existido. Por ejemplo, en el tiempo de los filósofos griegos Akhilleo y la tortuga, el cretano Epimenides, etc., siempre ha habido quebraderos de cabeza para filósofos y matemáticos. Pero XIX. Fue a finales del siglo XX cuando este problema alcanzó su máximo esplendor. En aquella época, debido a unas paradojas incomprensibles, las bases de las matemáticas se tambalearon y toda la casa estuvo a punto de caer. Si bien se ha conseguido explicar la mayoría de las paradojas, existen actualmente paradojas sin resolver. Otras han tenido muchas interpretaciones.
La paradoja que proponemos hoy no es de ellas, como se explicará al final del artículo, pero creemos que es una curiosidad. Esta paradoja se sitúa en el campo de las Estadísticas, concretamente en el cálculo de probabilidades.
Empecemos por plantear el problema, a decir mejor la pregunta: trazamos una circunferencia. También el triángulo equilátero inscrito en la circunferencia. La pregunta es: si trazamos una cuerda, ¿cuál es la probabilidad de que la longitud de la misma sea mayor que la parte del triángulo?
A continuación se presentan tres soluciones diferentes que responden a esta pregunta.
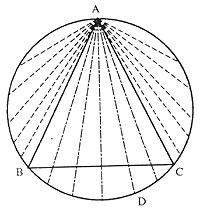
Marcamos la circunferencia y el triángulo equilátero. Sea el punto A un vértice del triángulo. Se considerarán las cuerdas trazadas desde el punto A. Como se puede apreciar en la figura, para que la zona de la cuerda sea más larga que la zona, debemos colocarla dentro del ángulo correspondiente al vértice A. Y en este caso, si los otros vértices del triángulo son B y C, el otro extremo de la cuerda (D) debe estar en el arco de la circunferencia entre los puntos B y C.
Si movemos el punto A por la circunferencia, tendríamos el mismo resultado. La longitud de la circunferencia es 2 r y la del arco BC 2 r/3. Definiendo la probabilidad como el cociente entre los casos favorables y los posibles, los casos a nuestro favor son 2 r/3 y los casos posibles 2 r. Por tanto, probabilidad
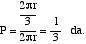
Para responder a la misma pregunta, esta vez actuaremos de otra manera. En este caso tomaremos un lado del triángulo y trazaremos las cuerdas paralelas a ese lado. Observando el diámetro perpendicular a estas cuerdas, se observa que las cuerdas más largas que el lado del triángulo ocupan medio diámetro. Teniendo en cuenta todo esto, se obtiene que los casos posibles son 2r y los casos favorables r. Por tanto, en este caso la probabilidad
Si se mueve el triángulo se obtiene el mismo resultado.
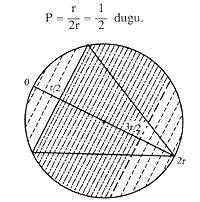
Esto no es suficiente y veamos la tercera respuesta. Tomemos ahora los puntos centrales de los lados del triángulo. Si hacemos girar el triángulo con respecto al centro de la circunferencia, estos puntos centrales de los lados describirán otra circunferencia. Para que las cuerdas sean más largas que las caras, los puntos centrales de las cuerdas deben estar dentro del círculo que delimita esta última circunferencia.
En este caso no hemos fijado ni el triángulo ni ningún punto. Por tanto, calcularemos directamente la probabilidad, siendo los casos favorables (r/2) 2 y los posibles r 2.
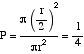
Para responder al mismo problema hemos obtenido tres resultados diferentes. ¿Cómo se explica esta paradoja?
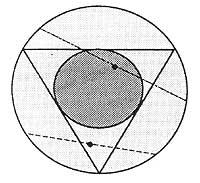
No debemos quedarnos en la piel. Si analizamos las tres conductas, en la primera hemos tomado la longitud de la circunferencia para calcular la probabilidad. En el segundo la longitud del diámetro y en el tercero la superficie del círculo. Es decir, en los tres casos hemos basado la probabilidad en diferentes espacios de probabilidad. Por tanto, los resultados obtenidos no son comparables.
Este problema es un ejemplo de la paradoja de Beltran.
Leamos la siguiente frase:
Los matemáticos obtienen diferentes números al calcular la probabilidad de ciertos sucesos. De hecho, los diferentes modelos matemáticos nos llevan a resultados diferentes, y el desacuerdo entre ellos es la causa de la discrepancia entre resultados.
El análisis más exhaustivo de los diferentes modelos estadísticos se presenta en el cuadro adjunto, con una instrumentación matemática más útil.
Veamos, pues, los modelos estadísticos correspondientes a tres planteamientos diferentes. En la notación que vamos a utilizar será un hecho que sea mayor que la diferencia KH = Corda.
Para fijar la cuerda en la primera vista basta con seleccionar un punto de la circunferencia, el otro vértice es el punto A. Por lo tanto, siendo esta elección totalmente aleatoria o aleatoria y comprendida entre [0,2 r], el modelo estadístico correspondiente es una distribución uniforme. Así, para calcular la probabilidad del suceso KH, los valores que pueden tomar las variables aleatorias deben estar en el intervalo [2 r/3, 3 r/3]. Por lo tanto:
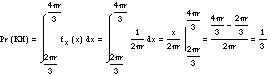
En el segundo planteamiento, es decir, cuando trazamos paralelos a un lado, se cumplirá el suceso KH sólo si seleccionamos un punto en el intervalo [r/2, 3r/2] en el diámetro asociado a los paralelos. A esta elección le corresponde otra variable aleatoria uniforme, pero ahora en el intervalo [0.2r]. La probabilidad del suceso GC se calcula como:
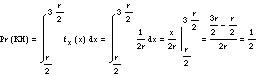
En el último punto de vista será mayor que el lado de la cuerda rayada, sólo si el punto medio de la cuerda está dentro del círculo pequeño. Dado que este punto está en el plano, tendrá dos coordenadas (x,y) y si situamos los ejes de coordenadas en el centro del círculo, el suceso GC x 2 +y 2 (r/2) se cumplirá cuando la ecuación 2 sea cierta. Hay que tener en cuenta que en este caso (X,Y) se trata de una variable aleatoria bidimensional cuyo campo es un gran círculo. Es decir, su función de densidad
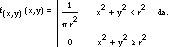
Teniendo en cuenta todo esto, podemos calcular la probabilidad del suceso GC de la siguiente manera: