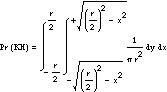Paradoxa de Kord
En general podem dir que la paradoxa és un raonament que ens contradiu, que pot ser real, fals o no l'un ni l'altre. Les paradoxes sempre han existit. Per exemple, en el temps dels filòsofs grecs Akhilleo i la tortuga, el cretano Epimenides, etc., sempre hi ha hagut maldecaps per a filòsofs i matemàtics. Però XIX. Va ser a la fi del segle XX quan aquest problema va aconseguir la seva màxima esplendor. En aquella època, a causa d'unes paradoxes incomprensibles, les bases de les matemàtiques es van trontollar i tota la casa va estar a punt de caure. Si bé s'ha aconseguit explicar la majoria de les paradoxes, existeixen actualment paradoxes sense resoldre. Unes altres han tingut moltes interpretacions.
La paradoxa que proposem avui no és d'elles, com s'explicarà al final de l'article, però creem que és una curiositat. Aquesta paradoxa se situa en el camp de les Estadístiques, concretament en el càlcul de probabilitats.
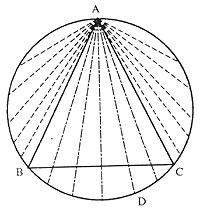
Comencem per plantejar el problema, a dir millor la pregunta: tracem una circumferència. També el triangle equilàter inscrit en la circumferència. La pregunta és: si tracem una corda, quina és la probabilitat que la longitud de la mateixa sigui major que la part del triangle?
A continuació es presenten tres solucions diferents que responen a aquesta pregunta.
Marquem la circumferència i el triangle equilàter. Sigui el punt A un vèrtex del triangle. Es consideraran les cordes traçades des del punt A. Com es pot apreciar en la figura, perquè la zona de la corda sigui més llarga que la zona, hem de col·locar-la dins de l'angle corresponent al vèrtex A. I en aquest cas, si els altres vèrtexs del triangle són B i C, l'altre extrem de la corda (D) ha d'estar en l'arc de la circumferència entre els punts B i C.
Si movem el punt Per la circumferència, tindríem el mateix resultat. La longitud de la circumferència és 2 r i la de l'arc BC 2 r/3. Definint la probabilitat com el quocient entre els casos favorables i els possibles, els casos al nostre favor són 2 r/3 i els casos possibles 2 r. Per tant, probabilitat
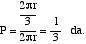
Per a respondre a la mateixa pregunta, aquesta vegada actuarem d'una altra manera. En aquest cas prendrem un costat del triangle i traçarem les cordes paral·leles a aquest costat. Observant el diàmetre perpendicular a aquestes cordes, s'observa que les cordes més llargues que el costat del triangle ocupen mig diàmetre. Tenint en compte tot això, s'obté que els casos possibles són 2r i els casos favorables r. Per tant, en aquest cas la probabilitat
Si es mou el triangle s'obté el mateix resultat.
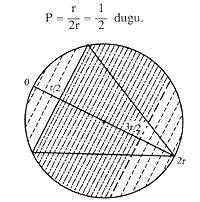
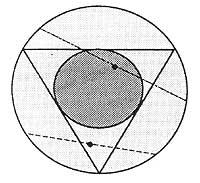
Això no és suficient i vegem la tercera resposta. Prenguem ara els punts centrals dels costats del triangle. Si fem girar el triangle respecte al centre de la circumferència, aquests punts centrals dels costats descriuran una altra circumferència. Perquè les cordes siguin més llargues que les cares, els punts centrals de les cordes han d'estar dins del cercle que delimita aquesta última circumferència.
En aquest cas no hem fixat ni el triangle ni cap punt. Per tant, calcularem directament la probabilitat, sent els casos favorables (r/2) 2 i els possibles r 2.
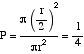
Per a respondre al mateix problema hem obtingut tres resultats diferents. Com s'explica aquesta paradoxa?
No hem de quedar-nos en la pell. Si analitzem les tres conductes, en la primera hem pres la longitud de la circumferència per a calcular la probabilitat. En el segon la longitud del diàmetre i en el tercer la superfície del cercle. És a dir, en els tres casos hem basat la probabilitat en diferents espais de probabilitat. Per tant, els resultats obtinguts no són comparables.
Aquest problema és un exemple de la paradoxa de Beltran.
Llegim la següent frase:
Els matemàtics obtenen diferents números en calcular la probabilitat de certs successos. De fet, els diferents models matemàtics ens porten a resultats diferents, i el desacord entre ells és la causa de la discrepància entre resultats.
L'anàlisi més exhaustiva dels diferents models estadístics es presenta en el quadre adjunt, amb una instrumentació matemàtica més útil.
Vegem, doncs, els models estadístics corresponents a tres plantejaments diferents. En la notació que utilitzarem serà un fet que sigui major que la diferència KH = Corda.
Per a fixar la corda en la primera vista n'hi ha prou amb seleccionar un punt de la circumferència, l'altre vèrtex és el punt A. Per tant, sent aquesta elecció totalment aleatòria o aleatòria i compresa entre [0,2 r], el model estadístic corresponent és una distribució uniforme. Així, per a calcular la probabilitat del succés KH, els valors que poden prendre les variables aleatòries han d'estar en l'interval [2 r/3, 3 r/3]. Per tant:
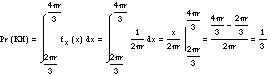
En el segon plantejament, és a dir, quan tracem paral·lels a un costat, es complirà el succés KH només si seleccionem un punt en l'interval [r/2, 3r/2] en el diàmetre associat als paral·lels. A aquesta elecció li correspon una altra variable aleatòria uniforme, però ara en l'interval [0.2r]. La probabilitat del succés GC es calcula com:
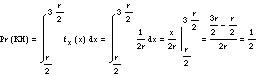
En l'últim punt de vista serà major que el costat de la corda ratllada, només si el punt mitjà de la corda està dins del cercle petit. Atès que aquest punt està en el pla, tindrà dues coordenades (x,i) i si situem els eixos de coordenades en el centre del cercle, el succés GC x 2 +i 2 (r/2) es complirà quan l'equació 2 sigui certa. Cal tenir en compte que en aquest cas (X,I) es tracta d'una variable aleatòria bidimensional el camp de la qual és un gran cercle. És a dir, la seva funció de densitat
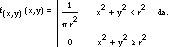
Tenint en compte tot això, podem calcular la probabilitat del succés GC de la següent manera: