Paradoxe de Kord
En général, nous pouvons dire que le paradoxe est un raisonnement qui nous contredit, qui peut être réel, faux ou pas l'un ou l'autre. Les paradoxes ont toujours existé. Par exemple, dans le temps des philosophes grecs Akhilleo et la tortue, le cretane Epimenides, etc., il y a toujours eu des cassures de tête pour les philosophes et les mathématiciens. Mais XIX. C'est à la fin du XXe siècle que ce problème a atteint son apogée. À cette époque, en raison de paradoxes incompréhensibles, les bases des mathématiques ont été chancelé et toute la maison était sur le point de tomber. Bien que la plupart des paradoxes aient été expliqués, il existe actuellement des paradoxes non résolus. D'autres ont eu beaucoup d'interprétations.
Le paradoxe que nous proposons aujourd'hui n'en est pas, comme expliqué à la fin de l'article, mais nous pensons que c'est une curiosité. Ce paradoxe se situe dans le domaine des statistiques, concrètement dans le calcul des probabilités.
Commençons par poser le problème, à mieux dire la question : nous traçons une circonférence. Aussi le triangle équilatéral inscrit dans la circonférence. La question est : si on trace une corde, quelle est la probabilité que sa longueur soit supérieure à celle du triangle ?
Voici trois solutions différentes qui répondent à cette question.
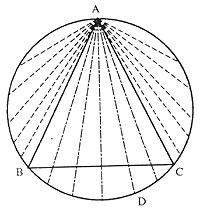
Nous marquons la circonférence et le triangle équilatéral. Soyez le point A un sommet du triangle. Les cordes tracées du point A seront considérées. Comme on peut le voir dans la figure, pour que la zone de la corde soit plus longue que la zone, on doit la placer à l'angle correspondant au sommet A. Et dans ce cas, si les autres sommets du triangle sont B et C, l'autre extrémité de la corde (D) doit être à l'arc de la circonférence entre les points B et C.
Si nous déplaçons le point A par la circonférence, nous aurions le même résultat. La longueur de la circonférence est 2 r et celle de l'arc BC 2 r/3. En définissant la probabilité comme le rapport entre les cas favorables et les possibles, les cas en notre faveur sont 2 r/3 et les cas possibles 2 r. Donc, probabilité
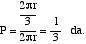
Pour répondre à la même question, cette fois, nous agirons autrement. Dans ce cas, nous prendrons un côté du triangle et tracerons les cordes parallèles de ce côté. En observant le diamètre perpendiculaire à ces cordes, on observe que les cordes plus longues que le côté du triangle occupent un demi-diamètre. Compte tenu de tout cela, on obtient que les cas possibles sont 2r et les cas favorables r. Donc, dans ce cas, la probabilité
Si vous déplacez le triangle, vous obtenez le même résultat.
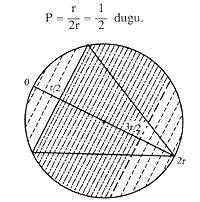
Ce n'est pas suffisant et voyons la troisième réponse. Prenons maintenant les points centraux des côtés du triangle. Si nous faisons tourner le triangle par rapport au centre de la circonférence, ces points centraux des côtés décriront une autre circonférence. Pour que les cordes soient plus longues que les faces, les points centraux des cordes doivent être dans le cercle qui délimite cette dernière circonférence.
Dans ce cas, nous n'avons fixé ni le triangle ni aucun point. Par conséquent, nous calculerons directement la probabilité, étant les cas favorables (r/2) 2 et les possibles r 2.
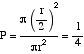
Pour répondre au même problème, nous avons obtenu trois résultats différents. Comment expliquer ce paradoxe?
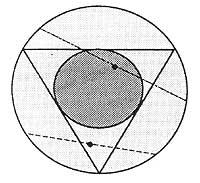
Nous ne devons pas rester sur la peau. Si nous analysons les trois conduites, dans la première nous avons pris la longueur de la circonférence pour calculer la probabilité. Dans le deuxième la longueur le diamètre et dans le troisième la surface du cercle. Autrement dit, dans les trois cas, nous avons basé la probabilité sur différents espaces de probabilité. Par conséquent, les résultats obtenus ne sont pas comparables.
Ce problème est un exemple du paradoxe de Beltran.
Lisons la phrase suivante:
Les mathématiciens obtiennent différents nombres en calculant la probabilité de certains événements. En fait, les différents modèles mathématiques nous conduisent à des résultats différents, et le désaccord entre eux est la cause de la divergence entre les résultats.
L'analyse la plus exhaustive des différents modèles statistiques est présentée dans le tableau ci-joint, avec une instrumentation mathématique plus utile.
Voyons donc les modèles statistiques correspondant à trois approches différentes. Dans la notation que nous allons utiliser sera un fait qui est supérieur à la différence KH = Corda.
Pour fixer la corde à la première vue, il suffit de sélectionner un point de la circonférence, l'autre sommet est le point A. Par conséquent, ce choix étant totalement aléatoire ou aléatoire et compris entre [0,2 r], le modèle statistique correspondant est une distribution uniforme. Ainsi, pour calculer la probabilité de l'événement KH, les valeurs que les variables aléatoires peuvent prendre doivent être dans l'intervalle [2 r/3, 3 r/3]. Par conséquent:
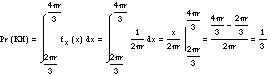
Dans la deuxième approche, c'est-à-dire lorsque nous traçons des parallèles d'un côté, l'événement KH ne sera accompli que si nous sélectionnons un point dans l'intervalle [r/2, 3r/2] dans le diamètre associé aux parallèles. À ce choix correspond une autre variable aléatoire uniforme, mais maintenant dans l'intervalle [0.2r]. La probabilité de l'événement GC est calculée comme:
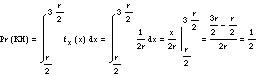
Dans le dernier point de vue sera plus grand que le côté de la corde rayée, seulement si le point médian de la corde est à l'intérieur du petit cercle. Puisque ce point est dans le plan, il aura deux coordonnées (x,y) et si nous plaçons les axes de coordonnées au centre du cercle, l'événement GC x 2 +y 2 (r/2) s'accomplira lorsque l'équation 2 est vraie. Notez que dans ce cas (X,Y) il s'agit d'une variable aléatoire bidimensionnelle dont le champ est un grand cercle. Autrement dit, sa fonction de densité
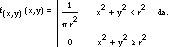
Compte tenu de tout cela, nous pouvons calculer la probabilité de l'événement GC comme suit: