Jeux mathématiques. Février 2014
Vous connaîtrez les images suivantes et associées
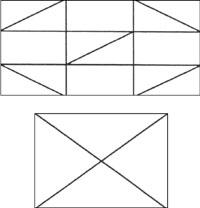
La proposition existante est de traverser toutes les droites par une seule ligne, sans traverser deux fois aucun d'eux.
Vous pouvez le voir dans l'image suivante
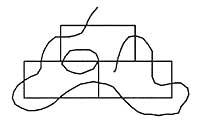
Comme après un essai, il est resté sans franchir une ligne droite. Essayé encore et encore, nous n'avons trouvé aucune résolution. Alors la question suivante nous vient à la tête: Cette proposition a-t-elle une résolution? Dans cet article, nous allons essayer de répondre à cette question.
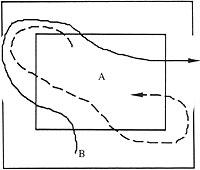
Pour cela, il est montré dans l'image
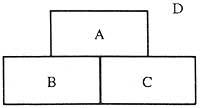
Comme nous les appellerons comarques. Et pour dire que nous sommes passés d'une région à l'autre, nous allons faire ce qui suit:
En passant de la région A à la zone B, nous écrivons AB. En passant de la région B à la région C BC, reliant ces deux étapes, c'est-à-dire en passant de A à B et de B à C nous écrivons ABC. Comme on le voit, le passage d'un droit est exprimé avec deux lettres. Mais passer deux lettres en trois. Jusqu'à présent, en passant d'une région à l'autre, nous n'avons pas dit pourquoi la direction doit arriver, car elle n'aura aucune importance dans ce raisonnement.
Compte tenu de tout cela, étant 12 le nombre de rectifications à passer dans notre image, nous devons écrire une succession de 13 lettres pour chercher une solution au problème. Cette séquence doit répondre à un certain nombre d'exigences, comme nous le verrons ci-dessous.
Entre les régions A et D il y a trois directes. Par conséquent, AD et DA doivent apparaître trois fois de suite. Cependant, le couple AB ou BA une seule fois, car entre les régions A et B il ya seulement un droit. Suivant le même raisonnement, les paires AC ou CA doivent apparaître une fois, les paires BC ou CB une fois et les paires BD ou DB et CD ou DC trois fois. Maintenant, la clé est de trouver une succession de 13 lettres avec ces combinaisons. Avant de commencer à chercher cette séquence, nous analyserons si théoriquement c'est possible ou non.
Si entre deux régions et les deux ont un seul droit, ces régions
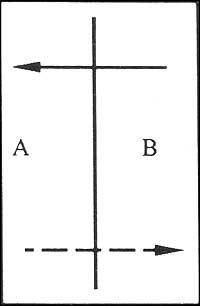
les lettres apparaîtront seulement une fois dans la séquence de lettres: AB ou BA. Mais si nous avions trois droites entre les deux régions, chaque lettre apparaîtrait deux fois: ABAB ou BABA. Et si nous avions cinq directs, nous verrions trois fois chaque lettre : ABABA ou BABABA.
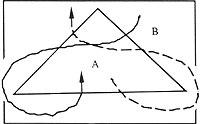
En général, le nombre impair n est le nombre de droites entre les deux régions.
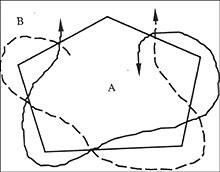
si chaque lettre apparaissait n+1/2 fois.
Que se passera-t-il lorsque le nombre d'amendements entre les deux régions sera pair ? Cas de cas
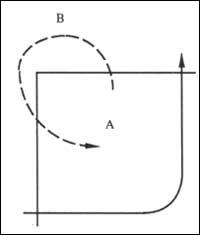
Dans ce cas, nous devrons tenir compte de la région dans laquelle nous avons commencé. Autrement dit, si nous avons deux directs, si nous commençons dans la région A nous aurons ABA, mais si nous commençons dans la région B nous obtiendrons BAB. Si nous avions quatre directs A
si nous commençons dans la région apparaîtrait ABABA et si nous commençons dans la région B on obtiendrait BABAB.
En général, si le nombre d'amendements (n) est pair, la lettre de la région dans laquelle la ligne démarre apparaît n/2 + 1 fois et la lettre de l'autre n/2 fois.
Ce que nous avons fait ici arrive avec deux limites. Mais quand il y a plus de deux régions, ces résultats ne changent pas, car en passant à un droit nous ne prenons en compte que deux régions, celles qui commencent et terminent la ligne.
En revenant à notre image, nous avons quatre régions. Les régions A, B et C sont délimitées par cinq droites. La région D, cependant, neuf directs. En appliquant ce que nous avons vu ci-dessus, nous pouvons écrire les régions dans la première colonne;

dans le second, le nombre d'amendements qui délimitent chaque région; et dans le troisième, le nombre de fois que chaque lettre doit apparaître. En additionnant les chiffres de la dernière colonne nous obtenons 14, c'est-à-dire que le nombre de fois que toutes les régions doivent apparaître est 14, mais comme nous l'avons dit au début nous devons trouver une succession de 13 lettres. Donc, dans ce cas, il n'y a pas de résolution.
En analysant ces problèmes en général, puisque le parcours doit être initié dans une région et en tenant compte du nombre de rectifications qui délimitent chaque région, nous déterminerons le nombre de fois que chaque lettre doit apparaître.
Si n est impair, la lettre apparaîtra n+1/2 fois. n/2 fois si n est paire, si vous démarrez depuis une autre région ou n/2 + 1 si vous commencez dans cette région. Compte tenu de ces résultats, on peut constater que si la somme de ces nombres est égale au nombre de droites plus un, le problème a une solution. Le cas où la somme est de nombre d'amendements a également une résolution, si la région dans laquelle elle est lancée est limitée par un nombre pair d'amendements, puisque dans ce cas la région indiquée apparaîtra n/2 + 1 fois. Dans le reste des cas, il n'y a pas de résolution.
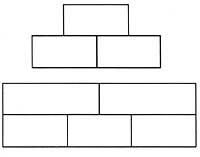
Il faut dire que cette évasion est la même que celle qui a été donnée au problème des ponts de Koenigsberg soulevé en son temps par le mathématicien Euler. Dans notre cas les ponts d'alors sont directs. Pour terminer, voici deux autres images pour que vous puissiez essayer de trouver la résolution.