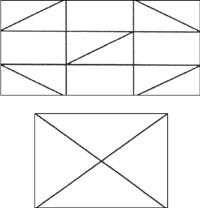
Mathematical games. February
You will know the following images and partners
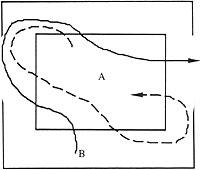
The existing proposal is to cross all the straight lines by a single line, without crossing any of them twice.
It can be seen in the following image
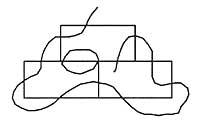
just like after a test has run out of crossing a straight line. Tried again and again, we have not found any resolution. Then the following question comes to mind: Is this proposal resolved? In this article we will try to answer this question.
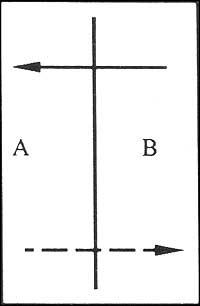
This is shown in the image
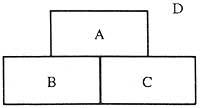
As we shall call them comarcas. And to say that we have moved from one region to another, we will do the following:
When passing from region A to zone B we wrote AB. Passing from region B to region C BC, joining these two steps, that is, passing from A to B and from B to C we write ABC. As you can see, the passage of a right is expressed in two letters. But pass two letters in three. So far, as we move from one region to another we have not said why direction we have to go, since it will have no importance in this reasoning.
Taking all this into account, with 12 being the number of rectifications to be passed in our image, we must write a sequence of 13 letters to find a solution to the problem. This sequence must meet a number of requirements, as we will see below.
Between regions A and D there are three direct. Therefore, AD and DA must appear three times in a row. However, the pair AB or BA only once, as between regions A and B there is only one right. Following the same reasoning, the AC or CA pairs must appear once, the BC or CB pairs once and the BD or DB and CD or DC pairs three times. Now the key is to find a succession of 13 letters with these combinations. Before we start looking for this sequence, we will analyze whether it is theoretically possible or not.
If between two regions and both we had only one right, these regions
letters would only appear once in the sequence of letters: AB or BA. But if we had three straight lines between the two regions, each letter would appear twice: ABAB or BABA. And if we had five directives, we would see three times each letter: ABABA or BABABA.
That is, in general, the odd number n is the number of lines between both regions
if each letter appeared n+1/2 times.
What will happen when the number of amendments between the two regions is even? Case Study
In this case we will have to take into account the region in which we started. That is, if we have two direct, if we start in the region A we will have ABA, but if we start in the region B we will get BAB. If we had four direct A
if we started in the region ABABA would appear and if we started in the region B would get BABAB.
In general, if the number of amendments (n) is even, the letter of the region in which the line starts will appear n/2 + 1 times and the letter of the other n/2 times.
What we have done here happens with two counties. But when there are more than two regions, these results do not change, since when moving to a right we only take into account two regions, which start and end the line.
Returning to our image, we have four counties. Regions A, B and C are delimited by five lines. District D, however, nine direct. Applying the above, we can write the regions in the first column;

in the second, the number of amendments that delimit each region; and in the third, the number of times each letter must appear. Adding the numbers in the last column we got 14, that is, the number of times that all regions should appear is 14, but as we said at the beginning we have to find a succession of 13 letters. Therefore, in this case there is no resolution.
Analyzing these problems in general, since the route should start in a region and taking into account the number of rectifications that delimit each region, we will determine the number of times each letter should appear.
If n is odd, the letter will appear n+1/2 times. n/2 times if n is even, if it starts from another region or n/2 + 1 if it starts in this region. Considering these results, you can check that if the sum of these numbers is equal to the number of straight plus one, the problem has a solution. The case in which the sum is number of amendments also has a resolution, if the region in which it starts is limited by an even number of amendments, since in this case the indicated region will appear n/2 + 1 times. In the rest of the cases there is no resolution.
It must be said that this evasion is the same that was given to the problem of the bridges of Koenigsberg raised in his day by the mathematician Euler. In our case the bridges then are direct. Finally, here are two more images for you to try to find the resolution.