Juegos matemáticos. Febrero
Conoceréis las siguientes imágenes y asociadas
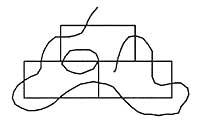
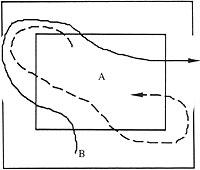
La propuesta existente es la de cruzar todos los rectos por una sola línea, sin cruzar dos veces ninguno de ellos.
Se puede ver en la siguiente imagen
al igual que después de una prueba se ha quedado sin cruzar una recta. Intentada una y otra vez, no hemos encontrado ninguna resolución. Entonces nos viene a la cabeza la siguiente pregunta: ¿Tiene resolución esta propuesta? En este artículo trataremos de dar respuesta a esta pregunta.
Para ello se muestra en la imagen
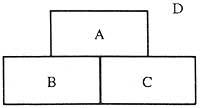
Como las denominaremos comarcas. Y para decir que hemos pasado de una región a otra, vamos a hacer lo siguiente:
Al pasar de la comarca A a la zona B escribimos AB. Al pasar de la comarca B a la comarca C BC, uniendo estos dos pasos, es decir, al pasar de A a B y de B a C escribimos ABC. Como se ve, el paso de un derecho lo expresamos con dos letras. Pero pasar dos letras en tres. Hasta ahora, al pasar de una región a otra no hemos dicho por qué dirección hay que pasar, ya que no tendrá importancia en este razonamiento.
Teniendo en cuenta todo esto, al ser 12 el número de rectificaciones que hay que pasar en nuestra imagen, debemos escribir una sucesión de 13 letras para buscar una solución al problema. Esta secuencia deberá cumplir una serie de requisitos, como veremos a continuación.
Entre las regiones A y D hay tres directas. Por lo tanto, AD y DA deben aparecer tres veces seguidas. Sin embargo, la pareja AB o BA sólo una vez, ya que entre las regiones A y B sólo hay un derecho. Siguiendo el mismo razonamiento, los pares AC o CA deben aparecer una vez, los pares BC o CB una vez y los pares BD o DB y CD o DC tres veces. Ahora la clave está en encontrar una sucesión de 13 letras con estas combinaciones. Antes de empezar a buscar esta secuencia, analizaremos si teóricamente es posible o no.
Si entre dos regiones y ambas tuviéramos un solo derecho, estas regiones
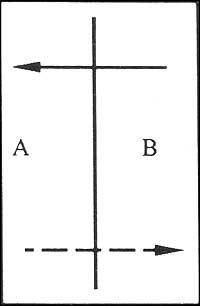
las letras sólo aparecerían una vez en la secuencia de letras: AB o BA. Pero si tuviéramos tres rectos entre ambas regiones, cada letra aparecería dos veces: ABAB o BABA. Y si tuviéramos cinco directos, veríamos tres veces cada letra: ABABA o BABABA.
Es decir, en general, el número impar n es el número de rectas entre ambas regiones
si cada letra apareciera n+1/2 veces.
¿Qué ocurrirá cuando el número de enmiendas entre las dos regiones sea par? Caso
En este caso tendremos que tener en cuenta la comarca en la que empezamos. Es decir, si tenemos dos directos, si empezamos en la comarca A tendremos ABA, pero si empezamos en la región B obtendremos BAB. Si tuviéramos cuatro directos A
si empezamos en la comarca aparecería ABABA y si empezamos en la comarca B se obtendría BABAB.
En general, si el número de enmiendas (n) es par, la letra de la región en la que se inicia la línea aparecerá n/2 + 1 veces y la letra del otro n/2 veces.
Lo que hemos hecho aquí ocurre con dos comarcas. Pero cuando hay más de dos regiones, estos resultados no cambian, ya que al pasar a un derecho sólo tenemos en cuenta dos regiones, las que empiezan y terminan la línea.
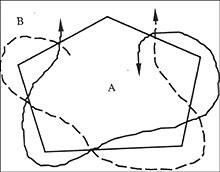
Volviendo a nuestra imagen, tenemos cuatro comarcas. Las regiones A, B y C están delimitadas por cinco rectas. La comarca D, sin embargo, nueve directos. Aplicando lo visto más arriba, podemos escribir las regiones en la primera columna;

en el segundo, el número de enmiendas que delimitan cada región; y en el tercero, el número de veces que debe aparecer cada letra. Sumando los números de la última columna conseguimos 14, es decir, el número de veces que deben aparecer todas las regiones es 14, pero como hemos dicho al principio tenemos que encontrar una sucesión de 13 letras. Por lo tanto, en este caso no hay resolución.
Analizando estos problemas en general, dado que el recorrido debe iniciarse en una región y teniendo en cuenta el número de rectificaciones que delimitan cada región, determinaremos el número de veces que debe aparecer cada letra.
Si n es impar, la letra aparecerá n+1/2 veces. n/2 veces si n es par, si se inicia desde otra región o n/2 + 1 si se inicia en esta región. Teniendo en cuenta estos resultados, se puede comprobar que si la suma de estos números es igual al número de rectas más uno, el problema tiene una solución. El caso en el que la suma es de número de enmiendas también tiene una resolución, si la región en la que se inicia está limitada por un número par de enmiendas, ya que en este caso la región indicada aparecerá n/2 + 1 veces. En el resto de los casos no hay resolución.
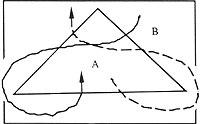
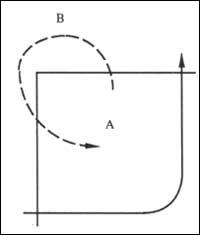
Hay que decir que esta evasión es la misma que se dio al problema de los puentes de Koenigsberg planteado en su día por el matemático Euler. En nuestro caso los puentes de entonces son directos. Para terminar, aquí tenéis dos imágenes más para que intentéis encontrar la resolución.