Jocs matemàtics. Febrer
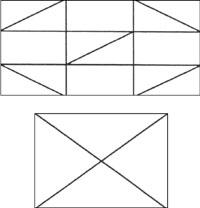
Coneixereu les següents imatges i associades
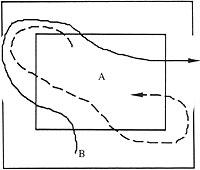
La proposta existent és la de creuar tots els rectes per una sola línia, sense creuar dues vegades cap d'ells. Es pot veure en la següent imatge
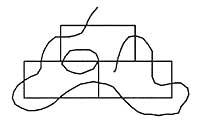
igual que després d'una prova s'ha quedat sense creuar una recta. Intentada una vegada i una altra, no hem trobat cap resolució. Llavors ens ve al capdavant la següent pregunta: Té resolució aquesta proposta? En aquest article tractarem de donar resposta a aquesta pregunta. Per a això es mostra en la imatge
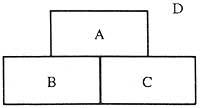
Com les denominarem comarques. I per a dir que hem passat d'una regió a una altra, farem el següent:
En passar de la comarca A a la zona B escrivim AB. En passar de la comarca B a la comarca C BC, unint aquests dos passos, és a dir, en passar d'a B i de B a C escrivim ABC. Com es veu, el pas d'un dret l'expressem amb dues lletres. Però passar dues lletres en tres. Fins ara, en passar d'una regió a una altra no hem dit per què direcció cal passar, ja que no tindrà importància en aquest raonament.
Tenint en compte tot això, en ser 12 el nombre de rectificacions que cal passar en la nostra imatge, hem d'escriure una successió de 13 lletres per a buscar una solució al problema. Aquesta seqüència haurà de complir una sèrie de requisits, com veurem a continuació.
Entre les regions A i D hi ha tres directes. Per tant, AD i DÓNA han d'aparèixer tres vegades seguides. No obstant això, la parella AB o BA només una vegada, ja que entre les regions A i B només hi ha un dret. Seguint el mateix raonament, els paris AC o CA han d'aparèixer una vegada, els parells BC o CB una vegada i els parells BD o DB i CD o DC tres vegades. Ara la clau està a trobar una successió de 13 lletres amb aquestes combinacions. Abans de començar a buscar aquesta seqüència, analitzarem si teòricament és possible o no.
Si entre dues regions i ambdues tinguéssim un solo dret, aquestes regions
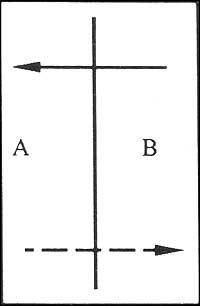
les lletres només apareixerien una vegada en la seqüència de lletres: AB o BA. Però si tinguéssim tres rectes entre totes dues regions, cada lletra apareixeria dues vegades: ABAB o BAVA. I si tinguéssim cinc directes, veuríem tres vegades cada lletra: ABABA o BABABA.
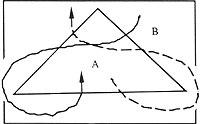
És a dir, en general, el nombre imparell n és el nombre de rectes entre totes dues regions
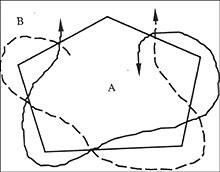
si cada lletra aparegués n+1/2 vegades.
Què ocorrerà quan el nombre d'esmenes entre les dues regions sigui parell? Cas
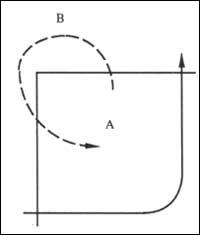
En aquest cas haurem de tenir en compte la comarca en la qual comencem. És a dir, si tenim dos directes, si comencem a la comarca A tindrem ABA, però si comencem a la regió B obtindrem BAB. Si tinguéssim quatre directes A
si comencem a la comarca apareixeria ABABA i si comencem a la comarca B s'obtindria BABAB.
En general, si el nombre d'esmenes (n) és parell, la lletra de la regió en la qual s'inicia la línia apareixerà n/2 + 1 vegades i la lletra de l'altre n/2 vegades.
El que hem fet aquí ocorre amb dues comarques. Però quan hi ha més de dues regions, aquests resultats no canvien, ja que en passar a un dret només tenim en compte dues regions, les que comencen i acaben la línia.
Tornant a la nostra imatge, tenim quatre comarques. Les regions A, B i C estan delimitades per cinc rectes. La comarca D, no obstant això, nou directes. Aplicant el vist més amunt, podem escriure les regions en la primera columna;

en el segon, el nombre d'esmenes que delimiten cada regió; i en el tercer, el nombre de vegades que ha d'aparèixer cada lletra. Sumant els números de l'última columna aconseguim 14, és a dir, el nombre de vegades que han d'aparèixer totes les regions és 14, però com hem dit al principi hem de trobar una successió de 13 lletres. Per tant, en aquest cas no hi ha resolució.
Analitzant aquests problemes en general, atès que el recorregut ha d'iniciar-se en una regió i tenint en compte el nombre de rectificacions que delimiten cada regió, determinarem el nombre de vegades que ha d'aparèixer cada lletra.
Si n és imparella, la lletra apareixerà n+1/2 vegades. n/2 vegades si n és parell, si s'inicia des d'una altra regió o n/2 + 1 si s'inicia en aquesta regió. Tenint en compte aquests resultats, es pot comprovar que si la suma d'aquests números és igual al nombre de rectes més un, el problema té una solució. El cas en el qual la suma és de nombre d'esmenes també té una resolució, si la regió en la qual s'inicia està limitada per un nombre parell d'esmenes, ja que en aquest cas la regió indicada apareixerà n/2 + 1 vegades. En la resta dels casos no hi ha resolució.
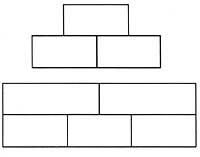
Cal dir que aquesta evasió és la mateixa que es va donar al problema dels ponts de Koenigsberg plantejat en el seu moment pel matemàtic Euler. En el nostre cas els ponts de llavors són directes. Per a acabar, aquí teniu dues imatges més perquè intenteu trobar la resolució.