1988/08/01 16. zenbakia

eu es fr en cat gl

• Itzulpen automatikoa
  • Español
  • Français
  • English
  • Català
  • Galego
  • Jatorrizkora itzuli

Elia Elhuyar

×

Aparecerá un contenido traducido automáticamente. ¿Deseas continuar?

Si No

Elia Elhuyar

×

Un contenu traduit automatiquement apparaîtra. Voulez-vous continuer?

Oui No

Elia Elhuyar

×

An automatically translated content item will be displayed. Do you want to continue?

Yes No

Elia Elhuyar

×

Apareixerà un contingut traduït automàticament. Vols continuar?

Si No

Elia Elhuyar

×

Aparecerá un contido traducido automaticamente. ¿Desexas continuar?

Se No

• Matematika

Paradoxos da xeometría

• Zabaldu:
• Twitter
• Facebook
• Emaila

Nun número anterior penetrámonos no mundo dos paradoxos da man da probabilidade. Aquí presentamos una colección de paradoxos que pode sorprender. Non utilizamos aquí a palabra sorprendente. A pesar de que os paradoxos son sorprendentes en si mesmas, esta sorprendencia sitúase normalmente nos razoamentos, pero nesta colección que traemos podemos atopala non só nos razoamentos, senón tamén na vista. Esta colección podería denominarse paradoxo xeométrico, xa que as probas dos enunciados propostos baséanse tanto en conceptos xeométricos como en imaxes. De momento deixaremos a clave dos paradoxos en mans dos lectores, deixando as resolucións paira outro número. (Si o lector deséxao, pode enviarnos as súas propias resolucións).

Comecemos a formulación de paradoxos.

Paradoxo 1

Respecto de una recta, pódense trazar dúas liñas perpendiculares a un punto exterior.

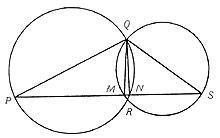
Debuxemos dúas circunferencias que se cruzan nos puntos Q e R. Desde o punto Q represéntanse os diámetros das circunferencias QP e QS. A continuación o segmento PS. Isto corta as circunferencias en dous puntos, M e N. (Ver imaxe).

Os triángulos PNQ e SMQ están inscritos en semicircunferencia, sendo un dos seus lados o diámetro. Por tanto, conclúese que os ángulos PNQ e SMQ deben ser correctos, ou o que é o mesmo os rectángulos QM e QN son unidos ao segmento PS, como queriamos demostrar.

Paradoxo 2

O ángulo recto é igual ao ángulo obtuso.

Sexa ABCD calquera rectángulo. Trazaremos polo punto B o segmento BE de lonxitude BC. Si representamos os puntos centrais dos rectángulos AB e DE, estes cruzaranse no punto P (Mira a imaxe). A partir deste punto P construiremos os reitores PA, PB, PD e PE. Nos triángulos DÁ e PUE as diferenzas DÁ son iguais,

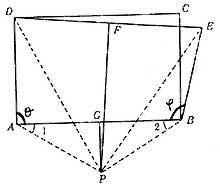
Porque así o eliximos. Tamén PA = PB e PD = PE, posto que o punto P atópase nas unións que pasan polo punto medio dos rectángulos DE e AB, o que significa que é distante por unha banda dos puntos A e B e por outro dos puntos D e E.

Dado que os lados destes dous triángulos son iguais respectivamente, os triángulos deben ser iguais. Por tanto, os ángulos DAP e EBP son iguais. Como polo outro lado o triángulo PBA é isósceles (PA = PB), os ángulos 1 e 2 son iguais. De aquí sacamos que o ángulo recto e o ángulo obtuso son iguais.

Paradoxo 3

Todos os puntos dun círculo atópanse na súa circunferencia.

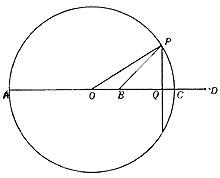
Sexa B Ou un punto do círculo con centro. Debuxaremos o diámetro AC desde o punto B. Prolongando o diámetro AC tomaremos o punto D para que se cumpra a seguinte proporción

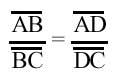
Construamos a BD unindo QP polo punto medio do segmento e representamos os rectángulos PO e PB polo punto P. Si o radio do círculo é r AB = r + OB e BC = r – OB, AD = r + OD e DC = OD – r. Proporción anterior por substitución desta igualdade

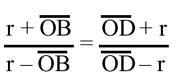
podemos escribir ou (r + OB) (OD – r) = (OD + r) (r – OB). OB tras operacións e simplificación. Obtemos OD = r ² e dado que paira a imaxe OB = QB – BQ e OD = OQ + QD, (OQ – BQ) (OQ + QD) = r ² . Pero como Q é o punto medio do segmento BD, BQ = QD, substituíndo esta última igualdade no anterior, obtemos r ² = OQ ^{2 – BQ 2} (1).

Aplicando o teorema de Pitágoras aos triángulos OQP e BQP:

OP ² = OQ ² + PQ ²
BP ² = BQ ² + PQ ²

Agora calculando por partes a diferenza entre ambas nivelaciones OP ² – BP ² = OQ ² – BQ ² , pero si OP = r é r ² – BP ² = OQ ² – BQ ² . Substituíndo esta igualdade (1) pola igualdade temos r ² = r ^{2 – BP 2} ou BP ² = 0. Por tanto, os puntos B e P deben coincidir, é dicir, o punto B debe estar na circunferencia.

Paradoxo 4

Todo triángulo é isósceles.

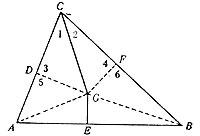
Sexa o triángulo ABC. Debuxemos a bisectriz do ángulo Cfl e o punto medio ao lado AB. Representaremos as unións GD e GF, respectivamente, cos lados AC e BC desde o punto G no que se cruzan ambas as liñas. Tamén os directos GA e GB. Os triángulos CGD e CGF son iguais, xa que a zona CG é común, 1fl = 2fl (construción) e 3fl = 4fl (rectas). Por tanto DG = GF. Nos triángulos GDA e GFB as rectas 5fl = 6fl, AG = BG (porque o triángulo IGP é isósceles) e como demostramos anteriormente DG = GF. Por tanto, GDA e GFB son os mesmos triángulos. Destas parellas de triángulos iguais dedúcese CD = CF e AD = BF. Agregando esta igualdade por partes AD + CD = BF + CF ou AC = BC, é dicir, o triángulo é isósceles.

Paradoxo 5

Comprobaremos que dous dos dous directos son iguais.

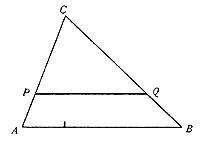
Sexa ABC calquera triángulo e PQ un rectángulo paralelo á beira AB (ver figura). Os triángulos ABC e PQC son similares. Por tanto

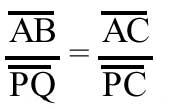
cúmprese a proporción. De aí AB . PC = AC . PQ. Multiplicando ambos os apartados por (AB – PQ) temos:

AB ² . PC – AB . PC . PQ = AC . PQ . AB – AC PQ ²

Nesta igualdade AB . PC . PQ e AC . PQ . Se cambiamos de sección AB:

AB ² . PC – AC. PQ . AB = AB . PC . PQ – AC. ^{Obtemos PQ 2.} Agora AB e PQ respectivamente extraendo o factor AB (AB . PC – AC. PQ) = PQ (AB . PC – AC. obterase (PQ) e (AB . PC – AC. Simplificando o PQ) en ambos os apartados, obtemos AB = PQ.

Paradoxo 6

Vexamos que 45° = 60° ou 3 = 4. Utilizando o lado AB do triángulo equilátero ABC como hipotenusa, construamos o triángulo recto ABD. Comprobamos que os ángulos ABC = 60º e ABD = 45º son iguais.

Na zona BC tomaremos o segmento BE de lonxitude BD. Sexa F, o punto medio do segmento AD. Debuxemos a liña FE recta ata que cortemos a extensión da zona AB no punto G. Uniremos directamente os puntos G e D. A continuación representaremos un rectángulo perpendicular aos puntos centrais das direccións GD e GE. Estas dúas rectas cortaranse no punto k. Asociaremos este punto K aos puntos G, D, E e B. (Ver imaxe). A función actual consiste en demostrar que os triángulos KDB e KBE son iguais. Isto débese a que KG = DC e KG = NC (xa que KDG e KGE son triángulos lisos). Por tanto NC = DC. Doutra banda, seleccionamos CV = BD e CJ é a parte común. Os dous triángulos, por tanto, son iguais. Por iso, vémonos uns a outros

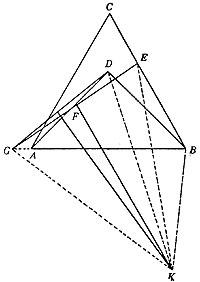
os ángulos correspondentes deben ser iguais, é dicir, os ángulos KBD e CCI son iguais. Se eliminamos a estes o ángulo VCC que é a parte común, obteremos os ángulos ABD e VC que buscabamos. Escribindo en radianes suporiamos /4 = /3 ou 3 = 4

Paradoxo 7

Neste último paradoxo inclúese a xeometría e a análise, e dentro da análise inclúese o concepto de limite. Na seguinte secuencia de imaxes aparece o problema que se produce no infinito, é dicir, ao tomar o límite.

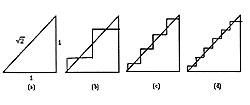
Como se observa na figura (a), existe un triángulo recto isósceles con catetos de 1 unidade, sendo a súa hipotenusa 2 unidade. As figuras (b), (c), (d) mostran os primeiros temas dunha sucesión de liñas crebadas. Por unha banda, estas liñas están cada vez máis preto da hipotenusa. Noutras palabras, o hipotenus e as liñas parécense cada vez máis. Doutra banda, todas as liñas rotas teñen una lonxitude de 2. Seguindo o procedemento, as seguintes liñas terían a mesma lonxitude. É dicir, seguindo as imaxes, o límite das liñas rotas é hipotenus. Con todo, seguindo as lonxitudes, a lonxitude do límite de liña é 2 (debido a que a sucesión de lonxitudes é constante). O paradoxo é que o límite de liña é hipotenusa, pero a lonxitude da hipotenusa non é 2 ; é 2.