Paradoxes de la geometria
En un número anterior ens endinsem en el món de les paradoxes de la mà de la probabilitat. Aquí presentem una col·lecció de paradoxes que pot sorprendre. No hem utilitzat aquí la paraula sorprenent. A pesar que les paradoxes són sorprenents en si mateixes, aquesta sorprendencia se situa normalment en els raonaments, però en aquesta col·lecció que portem podem trobar-la no sols en els raonaments, sinó també en la vista. Aquesta col·lecció podria denominar-se paradoxa geomètrica, ja que les proves dels enunciats proposats es basen tant en conceptes geomètrics com en imatges. De moment deixarem la clau de les paradoxes en mans dels lectors, deixant les resolucions per a un altre número. (Si el lector ho desitja, pot enviar-nos les seves pròpies resolucions).
Comencem el plantejament de paradoxes.
Paradoxa 1
Respecte a una recta, es poden traçar dues línies perpendiculars a un punt exterior.
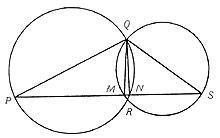
Dibuixem dues circumferències que es creuen en els punts Q i R. Des del punt Q es representen els diàmetres de les circumferències QP i QS. A continuació el segment PG. Això curta les circumferències en dos punts, M i N. (Veure imatge).
Els triangles PNQ i SMQ estan inscrits en semicircumferència, sent un dels seus costats el diàmetre. Per tant, es conclou que els angles PNQ i SMQ han de ser correctes, o cosa que és el mateix els rectangles QM i QN són units al segment PS, com volíem demostrar.
Paradoxa 2
L'angle recte és igual a l'angle obtús.
Sigui ABCD qualsevol rectangle. Traçarem pel punt B el segment BE de longitud BC. Si representem els punts centrals dels rectangles AB i DE, aquests es creuaran en el punt P (Mira la imatge). A partir d'aquest punt P construirem els rectors PA, PB, PD i PE. En els triangles DÓNA i PUE les diferències DÓNA són iguals,
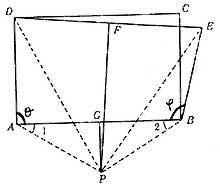
Perquè així ho hem triat. També PA = PB i PD = PE, ja que el punt P es troba en les unions que passen pel punt mitjà dels rectangles D'i AB, la qual cosa significa que és distant d'una banda dels punts A i B i per un altre dels punts D i E.
Atès que els costats d'aquests dos triangles són iguals respectivament, els triangles han de ser iguals. Per tant, els angles DAP i EBP són iguals. Com per l'altre costat el triangle PBA és isòsceles (PA = PB), els angles 1 i 2 són iguals. D'aquí traiem que l'angle recte i l'angle obtús són iguals.
Paradoxa 3
Tots els punts d'un cercle es troben en la seva circumferència.
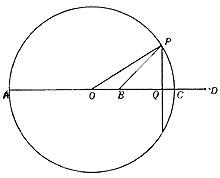
Sigui B O un punt del cercle amb centre. Dibuixarem el diàmetre AC des del punt B. Prolongant el diàmetre AC prendrem el punt D perquè es compleixi la següent proporció
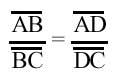
Construïm la BD unint QP pel punt mitjà del segment i representem els rectangles PO i PB pel punt P. Si el radi del cercle és r AB = r + OB i BC = r – OB, AD = r + OD i DC = OD – r. Proporció anterior per substitució d'aquestes igualtat
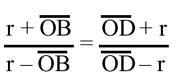
podem escriure o (r + OB) (OD – r) = (OD + r) (r – OB). OB després d'operacions i simplificació. Obtenim OD = r 2 i atès que per a la imatge OB = QB – BQ i OD = OQ + QD, (OQ – BQ) (OQ + QD) = r 2 . Però com a Q és el punt mitjà del segment BD, BQ = QD, substituint aquesta última igualtat en l'anterior, obtenim r 2 = OQ 2 – BQ 2 (1).
Aplicant el teorema de Pitàgores als triangles OQP i BQP:
OP 2 = OQ 2 + PQ 2
BP 2 = BQ 2 + PQ 2
Ara calculant per parts la diferència entre tots dos anivellaments OP 2 – BP 2 = OQ 2 – BQ 2 , però si OP = r és r 2 – BP 2 = OQ 2 – BQ 2 . Substituint aquesta igualtat (1) per la igualtat tenim r 2 = r 2 – BP 2 o BP 2 = 0. Per tant, els punts B i P han de coincidir, és a dir, el punt B ha d'estar en la circumferència.
Paradoxa 4
Tot triangle és isòsceles.
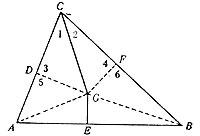
Sigui el triangle ABC. Dibuixem la bisectriu de l'angle Cfl i el punt mitjà del costat AB. Representarem les unions GD i GF, respectivament, amb els costats AC i BC des del punt G en el qual es travessen totes dues línies. També els directes GA i GB. Els triangles CGD i CGF són iguals, ja que la zona CG és comuna, 1fl = 2fl (construcció) i 3fl = 4fl (rectes). Per tant DG = GF. En els triangles GDA i GFB les rectes 5fl = 6fl, AG = BG (perquè el triangle IGP és isòsceles) i com hem demostrat anteriorment DG = GF. Per tant, GDA i GFB són els mateixos triangles. D'aquestes parelles de triangles iguals es dedueix CD = CF i AD = BF. Agregant aquestes igualtat per parts AD + CD = BF + CF o AC = BC, és a dir, el triangle és isòsceles.
Paradoxa 5
Comprovarem que dos dels dos directes són iguals.
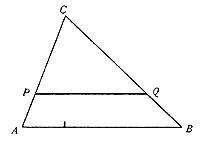
Sigui ABC qualsevol triangle i PQ un rectangle paral·lel al costat AB (veure figura). Els triangles ABC i PQC són similars. Per tant
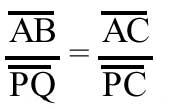
es compleix la proporció. D'aquí AB . PC = AC . PQ. Multiplicant tots dos apartats per (AB – PQ) tenim:
AB 2 . PC – AB . PC . PQ = AC . PQ . AB – AC PQ 2
En aquesta igualtat AB . PC . PQ i AC . PQ . Si canviem de secció AB:
AB 2 . PC – AC. PQ . AB = AB . PC . PQ – AC. Obtenim PQ 2. Ara AB i PQ respectivament extraient el factor AB (AB . PC – AC. PQ) = PQ (AB . PC – AC. s'obtindrà (PQ) i (AB . PC – AC. Simplificant el PQ) en tots dos apartats, obtenim AB = PQ.
Paradoxa 6
Vegem que 45° = 60° o 3 = 4. Utilitzant el costat AB del triangle equilàter ABC com a hipotenusa, construïm el triangle recte ABD. Comprovem que els angles ABC = 60° i ABD = 45° són iguals.
En la zona BC prendrem el segment BE de longitud BD. Sigui F, el punt mitjà del segment AD. Dibuixem la línia FE recta fins que tallem l'extensió de la zona AB en el punt G. Unirem directament els punts G i D. A continuació representarem un rectangle perpendicular als punts centrals de les direccions GD i GE. Aquestes dues rectes es tallaran en el punt k. Associarem aquest punt K als punts G, D, E i B. (Veure imatge). La funció actual consisteix a demostrar que els triangles KDB i KBE són iguals. Això es deu al fet que KG = DC i KG = NC (ja que KDG i KGE són triangles llisos). Per tant NC = DC. D'altra banda, hem seleccionat CV = BD i CJ és la part comuna. Els dos triangles, per tant, són iguals. Per això, ens veiem els uns als altres
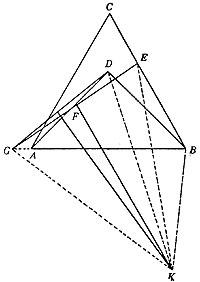
els angles corresponents han de ser iguals, és a dir, els angles KBD i CCI són iguals. Si eliminem a aquests l'angle VCC que és la part comuna, obtindrem els angles ABD e VC que buscàvem. Escrivint en radiants suposaríem /4 = /3 o 3 = 4
Paradoxa 7
En aquesta última paradoxa s'inclou la geometria i l'anàlisi, i dins de l'anàlisi s'inclou el concepte de limiti. En la següent seqüència d'imatges apareix el problema que es produeix en l'infinit, és a dir, en prendre el límit.
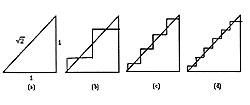
Com s'observa en la figura (a), existeix un triangle recte isòsceles amb catets d'1 unitat, sent la seva hipotenusa 2 unitat. Les figures (b), (c), (d) mostren els primers temes d'una successió de línies fetes fallida. D'una banda, aquestes línies estan cada vegada més prop de la hipotenusa. En altres paraules, l'hipotenus i les línies s'assemblen cada vegada més. D'altra banda, totes les línies trencades tenen una longitud de 2. Seguint el procediment, les següents línies tindrien la mateixa longitud. És a dir, seguint les imatges, el límit de les línies trencades és hipotenus. No obstant això, seguint les longituds, la longitud del límit de línia és 2 (pel fet que la successió de longituds és constant). La paradoxa és que el límit de línia és hipotenusa, però la longitud de la hipotenusa no és 2 ; és 2.





