Paradoxes de la géométrie
Dans un précédent numéro, nous entrons dans le monde des paradoxes de la main de probabilité. Voici une collection de paradoxes qui peut surprendre. Nous n'avons pas utilisé ici le mot surprenant. Même si les paradoxes sont surprenants en eux-mêmes, cette surprise se situe normalement dans les raisonnements, mais dans cette collection que nous apportons, nous pouvons la trouver non seulement dans les raisonnements, mais aussi dans la vue. Cette collection pourrait être appelée paradoxe géométrique, puisque les preuves des énoncés proposés sont basées aussi bien sur des concepts géométriques que sur des images. Pour l'instant, nous laisserons la clé des paradoxes aux mains des lecteurs, laissant les résolutions pour un autre numéro. (Si le lecteur le souhaite, il peut nous envoyer ses propres résolutions).
Commençons l'approche des paradoxes.
Paradoxe 1
Par rapport à une droite, on peut tracer deux lignes perpendiculaires à un point extérieur.
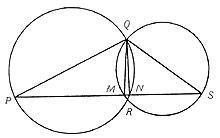
Dessinons deux circonférences croisées aux points Q et R. Du point Q, les diamètres des circonférences QP et QS sont représentés. Voici le segment PS. Cela coupe les circonférences en deux points, M et N. (Voir image).
Les triangles PNQ et SMQ sont inscrits en demi-circonférence, un des côtés étant le diamètre. On conclut donc que les angles PNQ et SMQ doivent être corrects, ou que les rectangles QM et QN sont liés au segment PS, comme nous voulions le démontrer.
Paradoxe 2
L'angle droit est égal à l'angle obtus.
Soyez ABCD n'importe quel rectangle. Nous tracerons par le point B le segment BE de longueur BC. Si nous représentons les points centraux des rectangles AB et DE, ceux-ci seront croisés au point P (voir l'image). A partir de ce point P nous construirons les recteurs PA, PB, PD et PE. Dans les triangles DA et PUE les différences DA sont égales,
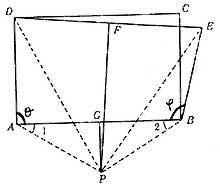
Parce que nous l'avons choisi. Aussi PA = PB et PD = PE, puisque le point P se trouve dans les jonctions passant par le milieu des rectangles DE et AB, ce qui signifie qu'il est éloigné d'un côté des points A et B et de l'autre des points D et E.
Puisque les côtés de ces deux triangles sont égaux respectivement, les triangles doivent être égaux. Les angles DAP et EBP sont donc identiques. Comme d'autre part le triangle PBA est isocèle (PA = PB), les angles 1 et 2 sont égaux. De là nous sortons que l'angle droit et l'angle obtus sont égaux.
Paradoxe 3
Tous les points d'un cercle sont dans leur circonférence.
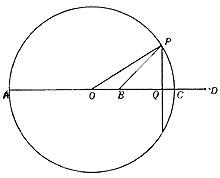
Soit B Ou un point du cercle avec centre. Nous dessinerons le diamètre AC du point B. En prolongeant le diamètre AC, nous prendrons le point D pour que la proportion suivante soit remplie
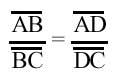
Nous construisons la BD en unissant QP par le milieu du segment et représentons les rectangles PO et PB par le point P. Si le rayon du cercle est r AB = r + OB et BC = r – OB, AD = r + OD et DC = OD – r. Proportion précédente par substitution de cette égalité
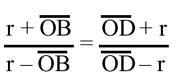
nous pouvons écrire ou (r + OB) (OD – r) = (OD + r) (r – OB). OB après opérations et simplification. Nous obtenons OD = r 2 et depuis pour l'image OB = QB – BQ et OD = OQ + QD, (OQ – BQ) (OQ + QD) = r 2 . Mais comme Q est le milieu du segment BD, BQ = QD, en remplaçant cette dernière égalité dans le précédent, nous obtenons r 2 = OQ 2 – BQ 2 (1).
Appliquer le théorème de Pythagore aux triangles OQP et BQP:
OP 2 = OQ 2 + PQ 2 BP 2 = BQ 2 + PQ 2
Maintenant, calculer la différence entre les deux niveaux OP 2 – BP 2 = OQ 2 – BQ 2 , mais si OP = r est r 2 – BP 2 = OQ 2 – BQ 2 . En remplaçant cette égalité (1) par l'égalité nous avons r 2 = r 2 – BP 2 ou BP 2 = 0. Par conséquent, les points B et P doivent correspondre, c'est-à-dire que le point B doit être dans la circonférence.
Paradoxe 4
Tout triangle est isocèle.
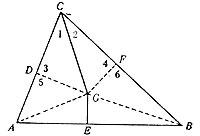
Soyez le triangle ABC. Dessinons la bissectrice de l'angle Cfl et le milieu du côté AB. Nous représenterons les jointures GD et GF, respectivement avec les côtés AC et BC du point G où les deux lignes sont croisées. Aussi les directs GA et GB. Les triangles CGD et CGF sont identiques, car la zone CG est commune, 1fl = 2fl (construction) et 3fl = 4fl (droite). Donc DG = GF. Dans les triangles GDA et GFB les droites 5fl = 6fl, AG = BG (parce que le triangle IGP est isocèle) et comme nous l'avons déjà montré DG = GF. Par conséquent, GDA et GFB sont les mêmes triangles. De ces couples de triangles égaux on déduit CD = CF et AD = BF. En ajoutant ces parts égales AD + CD = BF + CF ou AC = BC, c'est-à-dire que le triangle est isocèle.
Paradoxe 5
Nous vérifierons que deux des deux directs sont égaux.
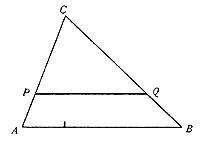
Soyez ABC tout triangle et PQ un rectangle parallèle au côté AB (voir figure). Les triangles ABC et PQC sont similaires. Donc, par conséquent,
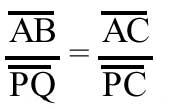
On accomplit la proportion. D'où AB . PC = AC . PQ. En multipliant les deux sections par (AB – PQ) nous avons:
AB 2 . PC – AB . PC . PQ = AC . PQ . AB – AC PQ 2
Dans cette égalité AB . PC . PQ et AC . PQ . Si nous changeons de section AB :
AB 2 . PC – AC. PQ . AB = AB . PC . PQ – AC. Nous obtenons PQ 2. Maintenant AB et PQ respectivement en extrayant le facteur AB (AB . PC – AC. PQ) = PQ (AB . PC – AC. sera obtenu (PQ) et (AB . PC – AC. En simplifiant le PQ) dans les deux sections, nous obtenons AB = PQ.
Paradoxe 6
Voyons que 45° = 60° ou 3 = 4. En utilisant le côté AB du triangle équilatéral ABC comme hypotense, nous construisons le triangle droit ABD. Nous vérifions que les angles ABC = 60º et ABD = 45º sont égaux.
Dans la zone BC nous prendrons le segment BE de longueur BD. Sea F, le milieu du segment AD. Dessinons la ligne FE droite jusqu'à ce que nous coupons l'extension de la zone AB au point G. Nous rejoindrons directement les points G et D. Nous représenterons ensuite un rectangle perpendiculaire aux points centraux des adresses GD et GE. Ces deux droites seront coupées au point k. Nous associerons ce point K aux points G, D, E et B. (Voir image). La fonction actuelle consiste à démontrer que les triangles KDB et KBE sont égaux. C'est parce que KG = DC et KG = NC (puisque KDG et KGE sont des triangles lisses). Donc NC = DC. D'autre part, nous avons sélectionné CV = BD et CJ est la partie commune. Les deux triangles sont donc égaux. Par conséquent, nous nous voyons les uns les autres
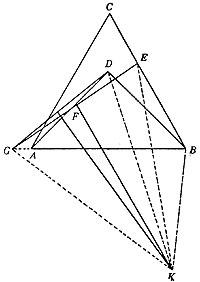
Les angles correspondants doivent être égaux, c'est-à-dire les angles KBD et CCI sont égaux. Si nous supprimons l'angle VCC qui est la partie commune, nous obtenons les angles ABD et VC que nous recherchions. En écrivant sur des radians nous supposerons /4 = /3 ou 3 = 4
Paradoxe 7
Ce dernier paradoxe inclut la géométrie et l'analyse, et le concept de limite est inclus dans l'analyse. Dans la séquence d'images suivante apparaît le problème qui se produit à l'infini, c'est-à-dire en prenant la limite.
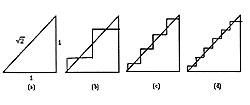
Comme le montre la figure (a), il existe un triangle droit isocèle avec des cathètes de 1 unité, son hypotense étant 2 unité. Les figures (b), (c), (d) montrent les premiers thèmes d'une succession de lignes brisées. D'une part, ces lignes sont de plus en plus proches de l'hypotense. En d'autres termes, l'hypotenus et les lignes semblent de plus en plus. D'autre part, toutes les lignes cassées ont une longueur de 2. En suivant la procédure, les lignes suivantes auraient la même longueur. C'est-à-dire, en suivant les images, la limite des lignes brisées est hipotenus. Cependant, suivant les longueurs, la longueur de la limite de ligne est 2 (parce que la succession des longueurs est constante). Le paradoxe est que la limite de ligne est hypotense, mais la longueur de l'hypotense n'est pas 2 ; il est 2.





