1988/08/01 16. zenbakia

eu es fr en cat gl

• Itzulpen automatikoa
  • Español
  • Français
  • English
  • Català
  • Galego
  • Jatorrizkora itzuli

Elia Elhuyar

×

Aparecerá un contenido traducido automáticamente. ¿Deseas continuar?

Si No

Elia Elhuyar

×

Un contenu traduit automatiquement apparaîtra. Voulez-vous continuer?

Oui No

Elia Elhuyar

×

An automatically translated content item will be displayed. Do you want to continue?

Yes No

Elia Elhuyar

×

Apareixerà un contingut traduït automàticament. Vols continuar?

Si No

Elia Elhuyar

×

Aparecerá un contido traducido automaticamente. ¿Desexas continuar?

Se No

• Matematika

Paradoxes of geometry

• Zabaldu:
• Twitter
• Facebook
• Emaila

In a previous issue we enter the world of paradoxes from the hand of probability. Here is a collection of paradoxes that can surprise you. We have not used here the surprising word. Although paradoxes are surprising in themselves, this surprises are usually placed in reasoning, but in this collection we bring we can find it not only in reasoning, but also in view. This collection could be called geometric paradox, since the evidence of the proposed statements is based on both geometric concepts and images. At the moment we will leave the key to paradoxes in the hands of readers, leaving the resolutions for another number. (If the reader wishes, he can send us his own resolutions.)

Let us begin the approach of paradoxes.

Paradox 1

Regarding a straight line, two perpendicular lines can be drawn to an outer point.

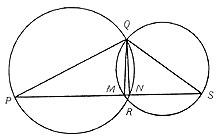
Let us draw two circles that cross in points Q and R. From point Q the diameters of the QP and QS circles are represented. Then the PS segment. This cuts the circles into two points, M and N. (See image).

The triangles PNQ and SMQ are inscribed in semicircle, being one of its sides the diameter. Therefore, it is concluded that the PNQ and SMQ angles must be correct, or what is the same the QM and QN rectangles are attached to the PS segment, as we wanted to demonstrate.

Paradox 2

The right angle is equal to the obtuse angle.

Be ABCD any rectangle. We will trace by point B the segment BE of length BC. If we represent the center points of the rectangles AB and DE, they will cross in point P (See image). From this point P will build the rectors PA, PB, PD and PE. In triangles DA and PUE the differences DA are equal,

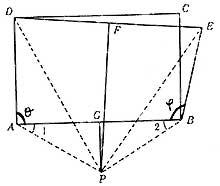
Because we have chosen it. Also PA = PB and PD = PE, since point P is in junctions passing through the midpoint of rectangles DE and AB, which means that it is distant on one side from points A and B and on the other from points D and E.

Since the sides of these two triangles are equal respectively, the triangles must be equal. Therefore, the DAP and EBP angles are equal. As on the other hand the triangle PBA is isosceles (PA = PB), angles 1 and 2 are equal. From here we draw that the right angle and the obtuse angle are equal.

Paradox 3

All points of a circle are in their circumference.

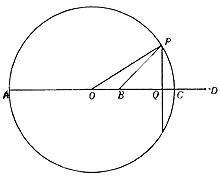
Be B Or a point of the circle with center. We will draw the AC diameter from point B. Extending the AC diameter we will take point D for the following proportion to be met

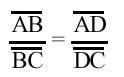
Let's build the DB by joining QP by the middle point of the segment and represent the PO and PB rectangles by point P. If the radius of the circle is r AB = r + OB and BC = r – OB, AD = r + OD and DC = OD – r. Previous proportion by substituting these equality

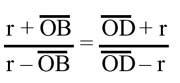
we can write or (r + OB) (OD – r) = (OD + r) (r – OB). OB after operations and simplification. We get OD = r ² and since for the image OB = QB – BQ and OD = OQ + QD, (OQ – BQ) (OQ + QD) = r ² . But since Q is the midpoint of the BD segment, BQ = QD, replacing this last equality in the previous one, we get r ² = OQ ^{2 – BQ 2} (1).

Applying the Pythagorean theorem to the OQP and BQP triangles:

OP ² = OQ ² + PQ ²
BP ² = BQ ² + PQ ²

Now calculating by parts the difference between both levels OP ² – BP ² = OQ ² – BQ 2, but if ^OP = r is r ² – BP ² = OQ ² – BQ ² . Substituting this equality (1) for equality we have r ² = r ^{2 – BP 2} or BP ² = 0. Therefore, points B and P must match, that is, point B must be in the circumference.

Paradox 4

Every triangle is isosceles.

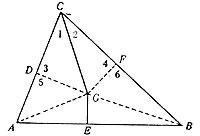
Be the triangle ABC. Let's draw the Cfl angle bisector and the midpoint of the AB side. We will represent the GD and GF joints, respectively, with the AC and BC sides from point G where both lines cross. Also direct GA and GB. The CGD and CGF triangles are the same, as the CG zone is common, 1fl = 2fl (construction) and 3fl = 4fl (straight). Therefore DG = GF. In the triangles GDA and GFB the straight 5fl = 6fl, AG = BG (because the triangle IGP is isosceles) and as we have shown previously DG = GF. Therefore, GDA and GFB are the same triangles. From these pairs of equal triangles, CD = CF and AD = BF are deducted. Adding these equality by parts AD + CD = BF + CF or AC = BC, that is, the triangle is isosceles.

Paradox 5

We will check that two of the two directives are equal.

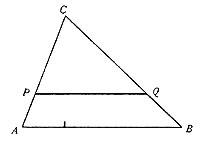
Be ABC any triangle and PQ a rectangle parallel to side AB (see figure). The ABC and PQC triangles are similar. Therefore

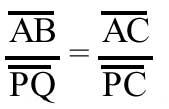
the proportion is met. Hence AB . PC = CA . PQ. Multiplying both sections by (AB – PQ) we have:

AB ² . PC – AB . PC . PQ = CA . PQ . AB – AC PQ ²

In this equality AB . PC . PQ and AC . PQ . If we change section AB:

AB ² . PC – AC. PQ . AB = AB . PC . PQ – AC. ^{We get PQ 2.} Now AB and PQ respectively extracting factor AB (AB . PC – AC. PQ) = PQ (AB . PC – AC. will be obtained (PQ) and (AB . PC – AC. By simplifying the PQ) in both sections, we obtain AB = PQ.

Paradox 6

Let us see that 45° = 60° or 3 = 4. Using the AB side of the ABC equilateral triangle as hypotenuse, we build the ABD right triangle. We check that the angles ABC = 60º and ABD = 45º are equal.

In the BC zone we will take the BE segment of BD length. Be F, the midpoint of the AD segment. Draw the straight FE line until we cut the extension of the AB zone at point G. We will directly connect points G and D. Below we will represent a rectangle perpendicular to the central points of the GD and GE directions. These two lines will be cut at point k. We will associate this point K to points G, D, E and B. (See image). The current function is to demonstrate that the KDB and KBE triangles are equal. This is because KG = DC and KG = NC (since KDG and KGE are smooth triangles). Therefore NC = DC. On the other hand, we have selected CV = BD and CJ is the common part. The two triangles, therefore, are equal. Therefore, we see each other

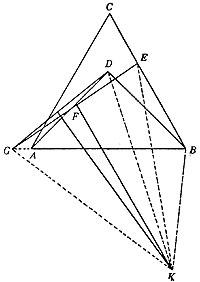
the corresponding angles must be equal, that is, the angles KBD and CCI are equal. If we remove to these the VCC angle that is the common part, we will get the ABD and VC angles we were looking for. Writing in radians we would assume /4 = /3 or 3 = 4

Paradox 7

This last paradox includes geometry and analysis, and includes the concept of limitation. In the next sequence of images appears the problem that occurs in infinity, that is, when taking the limit.

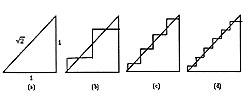
As seen in Figure (a), there is an isosceles right triangle with 1 unit cathetes, with its hypotenuse being 2 unit. Figures (b), (c), (d) show the first themes of a succession of broken lines. On the one hand, these lines are getting closer to hypotenuse. In other words, hypotenus and lines are increasingly similar. On the other hand, all broken lines have a length of 2. Following the procedure, the following lines would have the same length. That is, following the images, the limit of broken lines is hypotenus. However, following the lengths, the length of the line limit is 2 (because the succession of lengths is constant). The paradox is that the line limit is hypotenuse, but the length of the hypotenuse is not 2; it is 2.